By Paul Roggemans, Peter Cambell-Burns and Denis Vida
Abstract: A study of the 2021 Andromedids is presented based on the Global Meteor Network results. Andromedid orbits were identified during the interval in solar longitude 206° to 278°. Although rates were very low, three intervals with enhanced activity could be distinguished, a first dispersed at λʘ ~234°, a second more compact at λʘ ~239.4° and a final short enhancement at λʘ ~246.0°. The usual radiant drift caused by the rotation of the Earth around the Sun is partly compensated by the drift of the orbital elements. This explains the disagreement in radiant drift between different sources as these depend on the activity interval taken into consideration for the radiant drift. The orbital elements show a distinct evolution in time, the longitude of perihelion Π, the inclination i, and especially the perihelion distance q increase during the activity period. The eccentricity e decreases and the semi major axis a remains constant.
Introduction
The Andromedids have an impressive record in history books with most impressive meteor storms in the 19th century. During the 20th century this meteor shower seemed to have vanished and it was assumed that the dust had spread and did no longer cross the Earth orbit.
The parent comet 3D/Biela is a Jupiter-family comet first discovered in 1772 by Montaigne in France and at a later return in 1805 by Pons in France. It was Wilhelm von Biela at a later return in 1826 who obtained enough observations to prove this was a new periodic comet which had been observed before in 1772 and 1805. In 1846 the comet was observed with two separated nuclei. It was a last time seen in 1852 and all later attempts to rediscover it failed (Kronk, 1988).
The earliest known appearance of the Andromedids was witnessed by H.W. Brandes in the evening of 6 December 1798 when he counted about 100 meteors an hour for 4 hours. No information was mentioned about the radiant, but this outburst concerned most likely the Andromedids. Also on 7 December 1830, Abbe Raillard in France mentioned many meteors were seen without giving any further details. More information was obtained by Herrick in 1838 when large and splendid fireballs were seen on both December 6 and 7. Additional observing reports revealed that the radiant position was not far from Cassiopeia or perhaps near the cluster in the sword of Perseus with rates between 125 and 175 per hour. Eduard Heis observed the Andromedids on 6 December 1847 in Germany and obtained a radiant position at R.A. 21° and declination +54° (Kronk, 1988).
In the 1860s the link was made between comets and meteor showers. Edmond Weiss, Heinrich Louis d’Arrest and Johann Galle found independently that the meteoroids that caused the activity outbursts in 1798 and 1838 were associated with comet 3D/Biela. Edmond Weiss computed further and noticed the drift of the ascending node of the comet’s orbit and predicted that meteor activity caused by debris of this comet might be seen around 28 November 1872 from a radiant at R.A. 23.4° and declination +43.0° (Kronk, 1988).
The big surprise came in the evening of 27 November 1872 with a most spectacular meteor storm, described as a rain of fire with about 400 meteors every 1.5 minutes. The radiant could be precisely determined at R.A. 26.6° and declination +43.8°. The time of the maximum was estimated to be at November 27.84 UT when the meteors were too numerous to count. Predicted outbursts for 1878 and 1879 did not take place or went by unnoticed. Another possible outburst was predicted on short notice for 27 November 1885 and did materialize as observers with clear sky noticed immediately an acceptable activity. William Denning had observed meteor activity from the Andromedids with rates of about 100 per hour one night earlier. The evening of 27 November the number of meteors was too high and impossible to count them all with about one meteor every second. At the next expected passage of the parent comet, no such spectacular meteor storm was seen but rates were still several hundreds of meteors per hour on November 24. Andromedids displayed rates of about 100 meteors per hour on 24 November 1899 and about 20 per hour on 21 November 1904. No more activity from this shower was seen until 1940 when R.M. Dole in Maine, USA, reported an outburst with 30 meteors an hour on 15 November and J.P.M. Prentice reported rates of 5 meteors an hour between 27 November and 4 December (Kronk, 1988). No further visual activity from this shower was reported in the 20th century and the dust released by comet 3D/Biela was assumed no longer to intersect with the Earth orbit. Past Andromedid outbursts were modelled and described by Jenniskens and Vaubaillon (2007).
The Andromedids surprised with hourly rates of about 50 during the nights 3–5 December 2011 with a radiant at R.A. 18° and Declination +56°, the best activity in more than a century and again from the radiant position in Cassiopeia as it was in the beginning of the 19th century. The unexpected return was covered by the meteor radar CMOR in Canada (Wiegert et al., 2013) and the CAMS project (Jenniskens et al., 2016). A weak to moderate activity predicted to occur in 2018 did not materialize but the Andromedids surprised unexpectedly in 2021 with significant above normal Andromedid rates observed around 20 November by CAMS networks at the northern hemisphere (Jenniskens, 2022a). This broad activity enhancement was followed by a sharp peak on 28 November at λʘ = 245.887 ± 0.007° (Jenniskens, 2022b).
The Global Meteor Network (Vida et al., 2021) also recorded the 2021 Andromedid activity, and these results are presented in this analysis.
GMN 2021 Andromedid results
The Global Meteor Network identified 1034 orbits as Andromedids. This identification has been made based on a list of known meteor showers (Jenniskens et al., 2018) for orbits recorded within 1° in solar longitude of the known activity period, with the radiant within 3° relative to the known radiant position and with a geocentric velocity vg within an interval of 10% relative to the reference geocentric velocity (Moorhead et al., 2020).
Using an existing list of meteor showers with earlier determined radiant positions, activity periods and geocentric velocity, is helpful for a preliminary classification of shower meteor meteors, but this approach also creates a bias as the radiant positions, activity period and velocity range obtained will just confirm the reference that has been used for classification.
To consider all the orbits with the same criteria the author applied an iterative procedure starting from some initial reference orbit to identify all orbits that form a concentration of similar orbits which define the meteor shower. This method has been described before (Roggemans et al., 2019).
To identify all possible Andromedid orbits in an independent way all Andromedid orbits according to the GMN identification have been used to obtain a mean orbit according to the method described by Jopek et al. (2006). This mean orbit has then been used to run an iterative procedure to select all similar orbits, recompute the mean orbit and repeat this procedure until the iteration converges at a selection of similar orbits with the most representative mean orbit. To compare orbits on similarity mathematicians established different discrimination criteria, often abbreviated as D-criteria. The D-criteria that we use are these of Southworth and Hawkins (1963), Drummond (1981) and Jopek (1993) combined. The oldest and most popular D-criterion DSH, established by Southworth and Hawkins, proves often too tolerant and unsuitable for short period orbits near the ecliptic. It is not unusual that orbits which are very similar according to DSH, fail for another D-criteria such as that of Drummond or DD.
To distinguish dispersed and compact orbits we define five classes with different threshold levels of similarity, groups of orbits with comparable degree of dispersion. These should help to visualize the degree of dispersion and compactness within the meteoroid stream. The different classes of similarity are defined as follows:
- Low: DSH < 0.25 & DD < 0.105 & DH < 0.25;
- Medium low: DSH < 0.2 & DD < 0.08 & DH < 0.2;
- Medium high: DSH < 0.15 & DD < 0.06 & DH < 0.15;
- High: DSH < 0.1 & DD < 0.04 & DH < 0.1;
- Very high: DSH < 0.05 & DD < 0.02 & DH < 0.05.
The low threshold class with DD < 0.105 represents the most dispersed particles which may include sporadics with pure chance similarity. The very strong threshold class with DD < 0.02 represents the core of the dust trail with almost identical orbits. For readability reasons we refer to these classes using only the Drummond DD notification.
To limit the dataset in volume all 2021 GMN orbits were chosen between 20 October 2021 and 31 December 2021, in total 76570 orbits. 1954 orbits were identified to fulfill the low threshold criteria, registered between 20 October 2021 (λʘ = 207.3°) and 29 December 2021 (λʘ = 278.0°). 195 of these fulfilled the very high threshold criteria, registered between 13 and 26 November 2021
For a better comparison between results based on orbit similarity criteria and the shower identification based on the GMN identification method (radiant position and velocity), the similarity criteria were applied on the dataset with the 1034 preliminary GMN identified Andromedids. The mean orbit of these 1034 Andromedids has been used as reference orbit. Four orbits failed to fulfill even the low threshold criteria, the remaining 1030 GMN Andromedids were classified according to the different similarity classes.
Activity profile
A simple approach to obtain an activity profile is to count the number of recorded Andromedid orbits per time interval. To eliminate the influence of variable weather circumstances and different camera coverage for different time zones, we use the number of sporadic orbits without shower meteors to calibrate the Andromedid number of orbits for each time interval. This leaves the influence of the zenith distance of the Andromedid radiant as only factor that influences the number of Andromedids per time interval. The zenith distance factor cannot be determined for a mixture of orbits obtained for many different geographic locations mixed in each time interval. Statically we can just assume that the mixture of radiant distances in each interval will tend to average out the influence of the zenith distance.
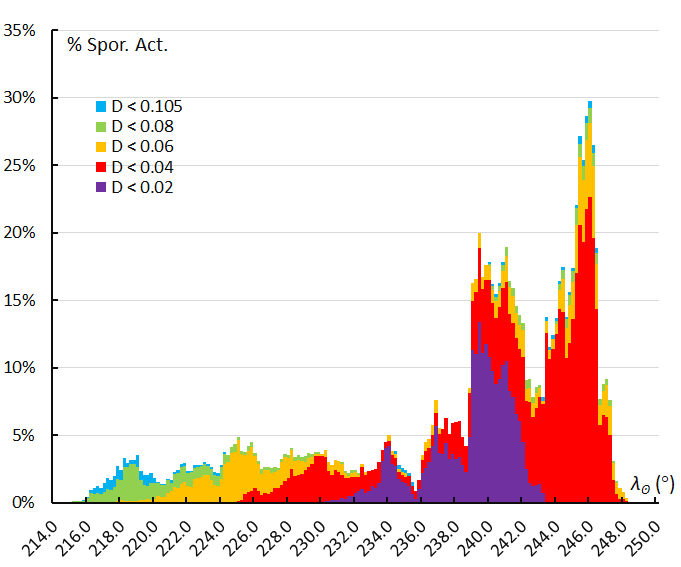
Figure 1 – Activity profile with the number of Andromedid orbits defined by the GMN shower identification method, expressed as a percentage relative to the number of sporadic orbits recorded during the same interval. The different similarity classes are color coded.
Figure 1 shows the resulting activity profile using a sampling interval of 1.1° in solar longitude, skipping 0.2° forward in solar longitude for each sampling interval. The width of the sampling interval has been chosen to smooth statistical fluctuations and still to maintain enough detail of the activity variation during the transit of the Earth through the Andromedid dust. The mean orbit used for the similarity criteria was obtained at the median value of the solar longitude of all GMN identified Andromedid orbits (λʘ = 240.6°). It is obvious that this mean reference orbit represents mainly the orbits around λʘ = 240.6° with many very high threshold similarities marked in purple in Figure 1. The earliest recorded Andromedid orbits have low similarity with this reference orbit and the profile in Figure 1 ends abruptly at about λʘ = 248° before the last peak on 29–30 November was completely ended. It is obvious that the activity period defined in the GMN reference table for shower identification ends too soon.
The abrupt end of the Andromedid activity period in the GMN reference list of meteor showers is to some extent compensated by the recorded December psi Cassiopeiids (DPC#446) which are in fact nothing other than Andromedids which were renamed at the 2011 Andromedid outburst in early December when the radiant was situated in the constellation of Cassiopeia.
Looking at the same activity profile based on the shower identification with orbit similarity criteria (Figure 2), the first possible Andromedid orbits were detected ten days earlier than with the GMN shower identification. Possible Andromedid orbits were detected during one month after the last Andromedid orbit identified by GMN. The main shape of the activity profile is visible in the two graphs. A first enhanced Andromedid activity appeared roughly between 227° < λʘ < 236° with a first modest peak at λʘ = 234° (2021, November 16, 11h UT). A second component of enhanced activity can be seen in the interval 236° < λʘ < 242.6° with a peak at λʘ = 239.4° (2021, November 21, 20h UT). The sharpest and highest activity occurred in the interval 243° < λʘ < 247.2° with a sharp peak at λʘ = 246.0° (2021, November 28, 08h UT). Before and after these three intervals only few and dispersed Andromedid orbits were recorded.
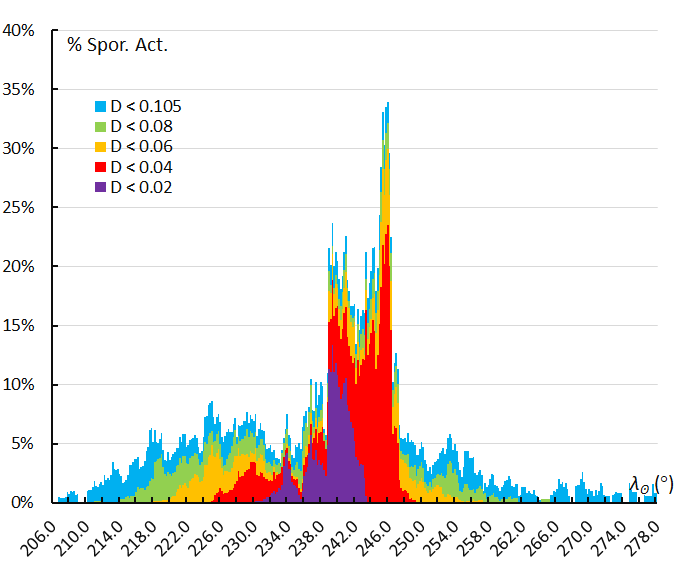
Figure 2 – Activity profile with the number of Andromedid orbits according to the orbit similarity criteria, expressed as a percentage relative to the number of sporadic orbits recorded during the same interval. The different similarity classes are color coded.
The activity profile based on numbers of orbits provides no precise data on the level of the shower activity in terms of zenithal hourly rates but the shape of the profile provides sufficient evidence for the layered structure of the Andromedid meteoroid stream and the approximate times of the different maxima. It is obvious that the Andromedids are a complex meteoroid stream with multiple superimposed dust trails embedded among widely dispersed particles that encounter the Earth orbit during a period of more than two months.
Radiant structure
The long duration activity period of the Andromedids suggests a significant radiant drift in geocentric equatorial coordinates. However, the values quoted in literature are not in agreement. Jenniskens (2006) lists Δα = 0.63°and Δδ = +0.33°, SonotaCo (2009), Δα = 0.12°and Δδ = +0.30°, Jenniskens et al. (2016) Δα = 1.00°and Δδ = +0.37° and this study resulted in Δα = 0.19°and Δδ = +0.75°. Looking at Figure 3 the radiant drift doesn’t show up as expected. The pattern of the radiant drift during the Andromedid activity displays a shape of a crescent. During the first part of the Andromedid activity the radiant drift shows a normal increase in Right Ascension and declination, while the declination continues to increase the Right Ascension remains constant and decreases towards the end of the activity period. The large differences in radiant drift values found in literature can be simply explained as these values depend on the activity interval on which the radiant drift has been obtained. Looking at the 1954 Andromedid orbits identified with the orbit similarity criteria (Figure 4) this plot displays the same crescent shape. The December psi Cassiopeiids marked as triangles in Figure 3 and many of the sporadic orbits according to the GMN shower identification were identified as Andromedids by the orbit similarity method.
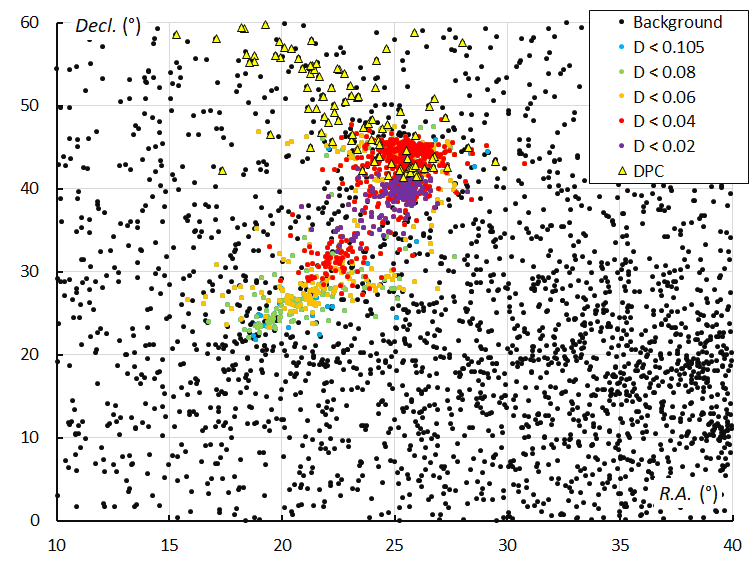
Figure 3 – The Andromedid radiants in equatorial geocentric coordinates based on the GMN shower identification, color coded according to the orbit similarity criteria. The triangles indicate the Andromedids which were identified as December psi Cassiopeïds (DPC#446).
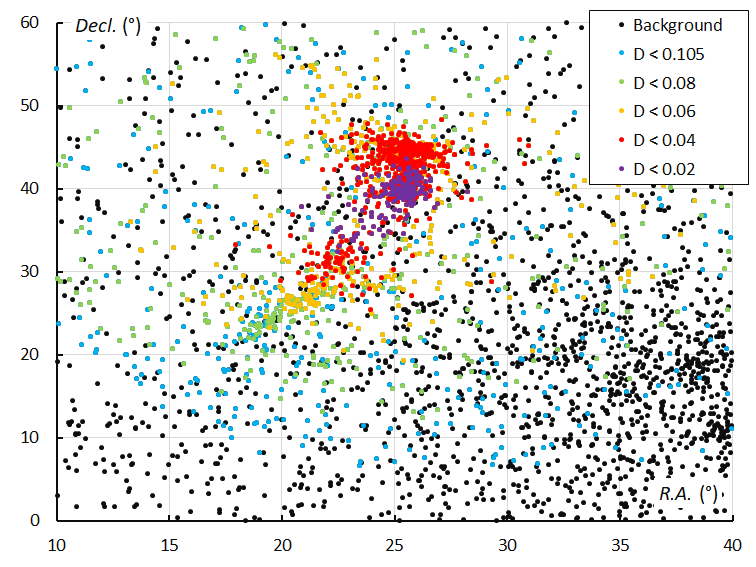
Figure 4 – The Andromedid radiants in equatorial geocentric coordinates based on the orbit similarity shower identification, color coded according to the orbit similarity criteria. The December psi Cassiopeïds (DPC#446) orbits from Figure 3 are detected as Andromedids.
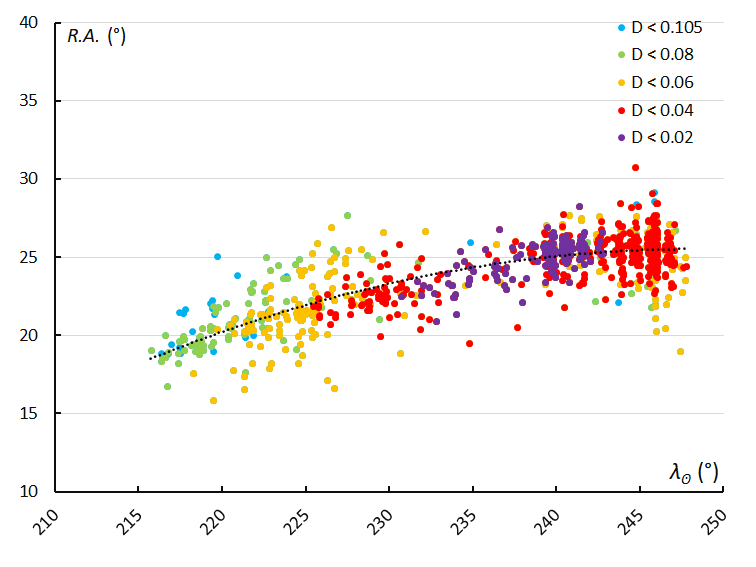
Figure 5 – The radiant drift in Right Ascension, based on the GMN shower identification.
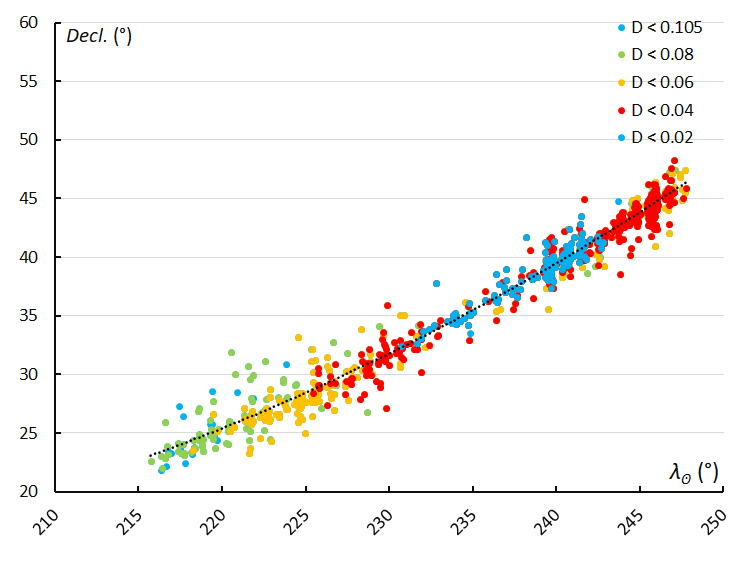
Figure 6 – The radiant drift in declination, based on the GMN shower identification.
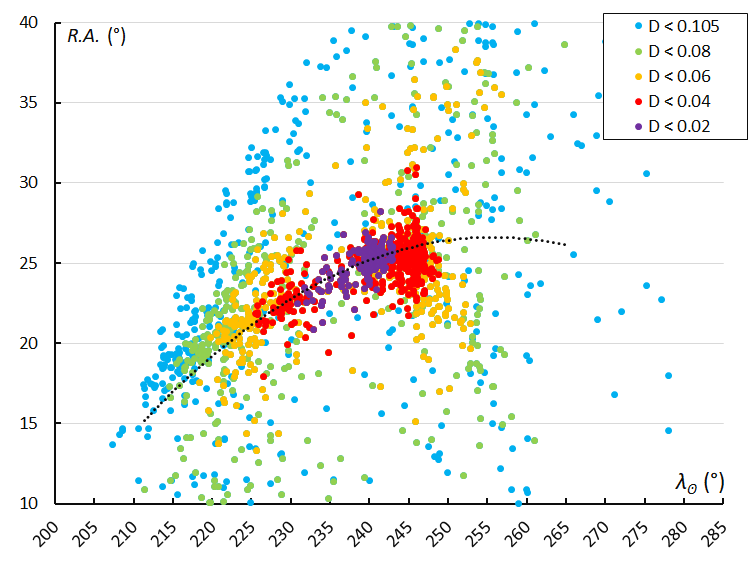
Figure 7 – The radiant drift in Right Ascension, based on the orbit similarity shower identification.
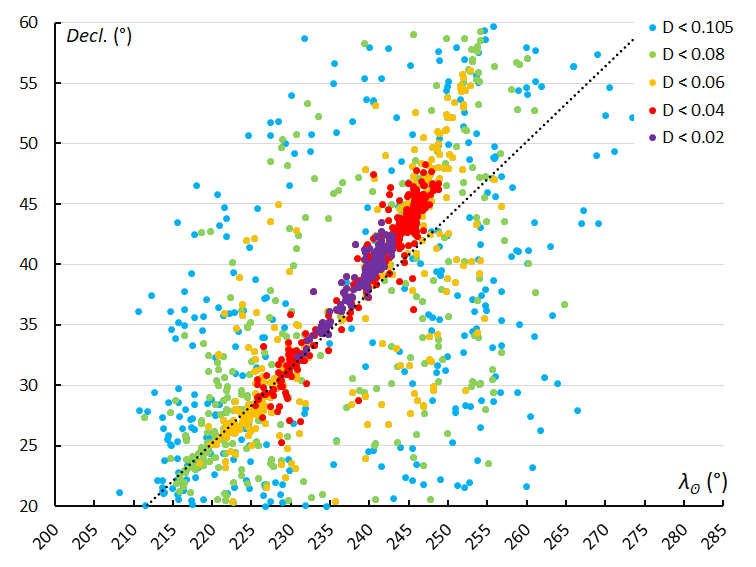
Figure 8 – The radiant drift in declination, based on the orbit similarity shower identification.
The radiant drift in Right Ascension in this case should not be described with an ordinary linear regression, but rather with a second order polynomial to fit the decreasing drift in function of the solar longitude (Figure 5). The radiant drift in declination shows an almost linear increase during the activity period (Figure 6). The unusual radiant drift behavior is even better visible in the plot with the orbit similarity shower identification with a longer activity period but ignoring the low similarity cases (Figure 7).
With the much longer activity period detected with the orbit similarity shower identification, the radiant drift in declination increases significantly in the second half of the activity period after a rather constant drift in declination during the first half (Figure 8). The third and last part of the activity period determined by orbit similarity identification, includes the orbits that were identified by GMN as December psi Cassiopeiids (DPC#446).
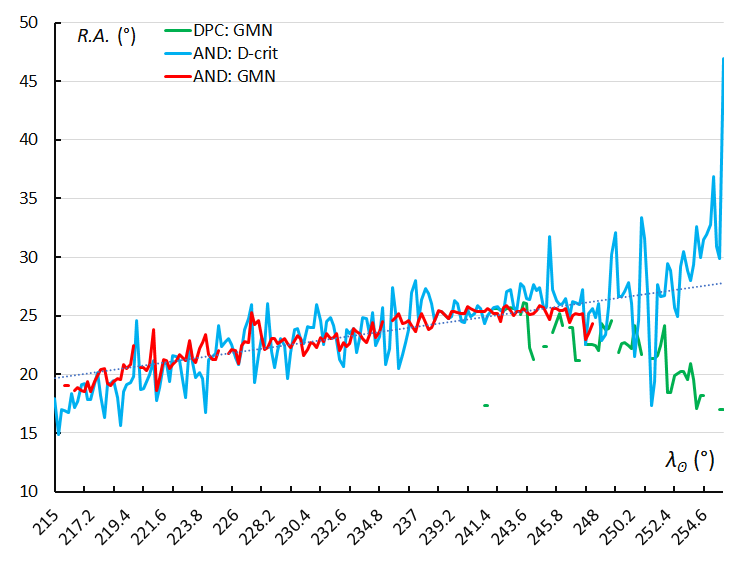
Figure 9 – The radiant drift in Right Ascension, using the sliding mean of the Right Ascension computed for a time interval of 0.4° in solar longitude in steps of 0.2°. The GMN shower identification is marked in red for the Andromedids and in green for the December psi Cassiopeiids, the Andromedids according to the orbit similarity identification are marked in blue.
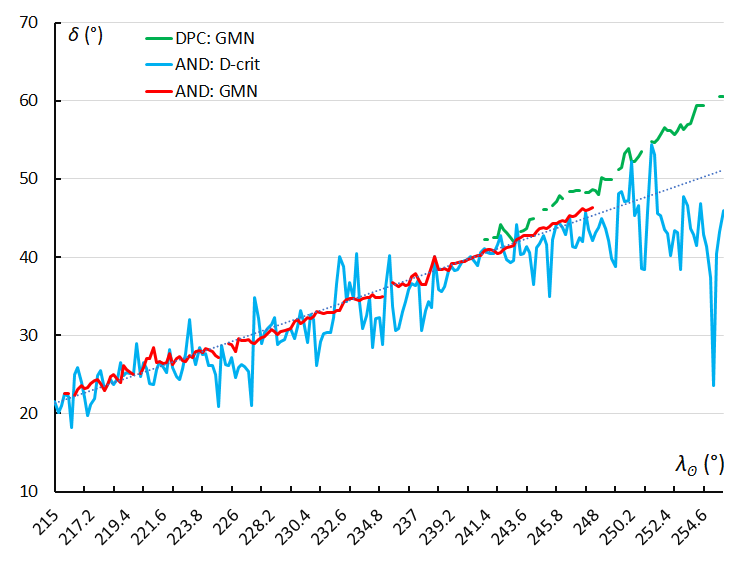
Figure 10 – The radiant drift in declination, using the sliding mean of the declination computed for a time interval of 0.4° in solar longitude in steps of 0.2°. The GMN shower identification is marked in red for the Andromedids and in green for the December psi Cassiopeiids, the Andromedids according to the orbit similarity identification are marked in blue.
To reduce the scatter on the Right Ascension and declination for each interval in solar longitude, the average value has been calculated for intervals of 0.4° in solar longitude, using steps of 0.2°. The values for the radiant positions of Andromedids according to the GMN shower identification (red) display very little scatter compared to the values according to the orbit similarity identification (blue) (Figures 9 and 10).
The December psi Cassiopeiids (DPC) identified by the GMN method display a deviant behavior as the radiant regresses in Right Ascension (Figure 9) and increases more in declination (Figure 10). These radiants were detected by the orbit similarity method as ordinary Andromedids among plenty of other Andromedids identified after the assumed activity period in the reference list used for the GMN identification. DPC orbits display a slightly different radiant drift compared to the ordinary Andromedids which appear with a very large scatter on the radiant positions.
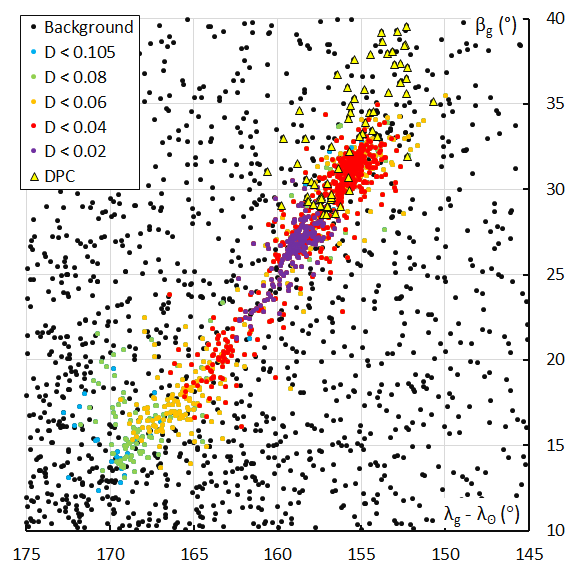
Figure 11 – The Andromedid radiants in Sun-centered geocentric ecliptic coordinates based on the GMN shower identification, color coded according to the orbit similarity criteria. The triangles indicate the Andromedids which were identified as December psi Cassiopeiids.
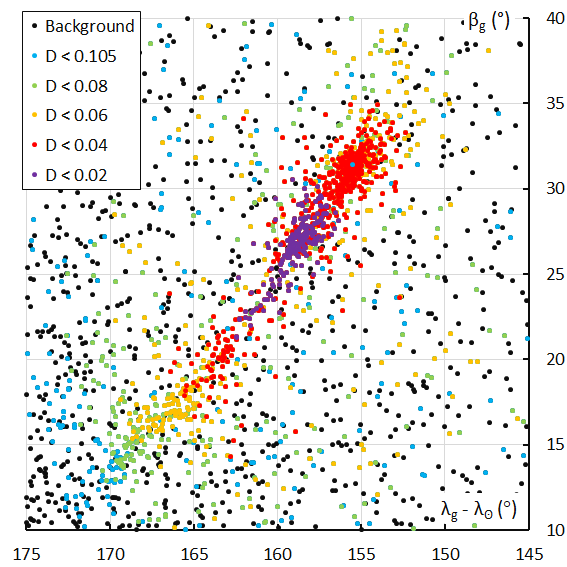
Figure 12 – The Andromedid radiants in Sun-centered geocentric ecliptic coordinates based on the orbit similarity shower identification, color coded according to the orbit similarity criteria. The December psi Cassiopeiids (DPC#446) orbits from Figure 11 are detected as Andromedids.
The usual way to look at a radiant without the radiant drift caused by the rotation of the Earth around the Sun is to plot the Sun-centered geocentric ecliptic coordinates. For most showers this results in a compact concentration of radiant points. For the Andromedids this results in a completely different picture with a long stretched radiant area. This means that the particles don’t move on parallel orbits but encounter the Earth at different angles to an extent that the usual radiant drift is compensated. The plots obtained with the GMN identification, and the orbit similarity identification can be compared in Figures 11 and 12.
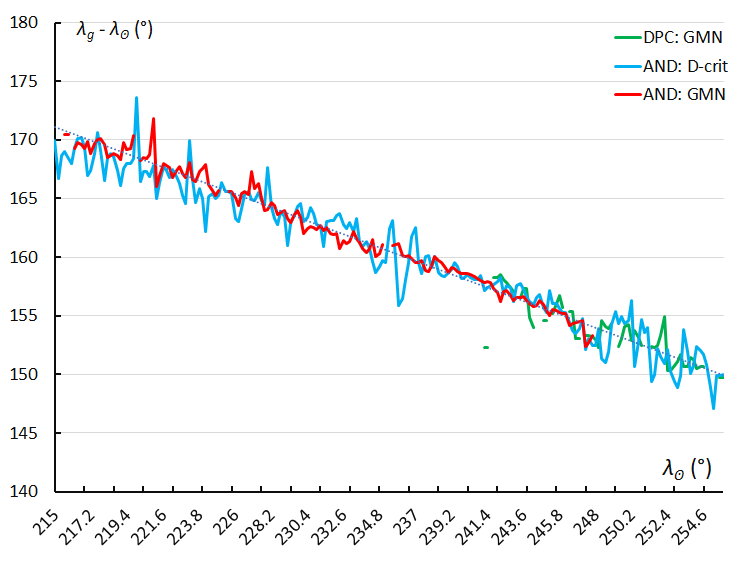
Figure 13 – The radiant drift in Sun-centered geocentric ecliptic longitude, using the sliding mean of the Sun-centered geocentric ecliptic longitude computed for a time interval of 0.4° in solar longitude in steps of 0.2°. The GMN shower identification is marked in red for the Andromedids and in green for the December psi Cassiopeiids, the Andromedids according to the orbit similarity identification are marked in blue.
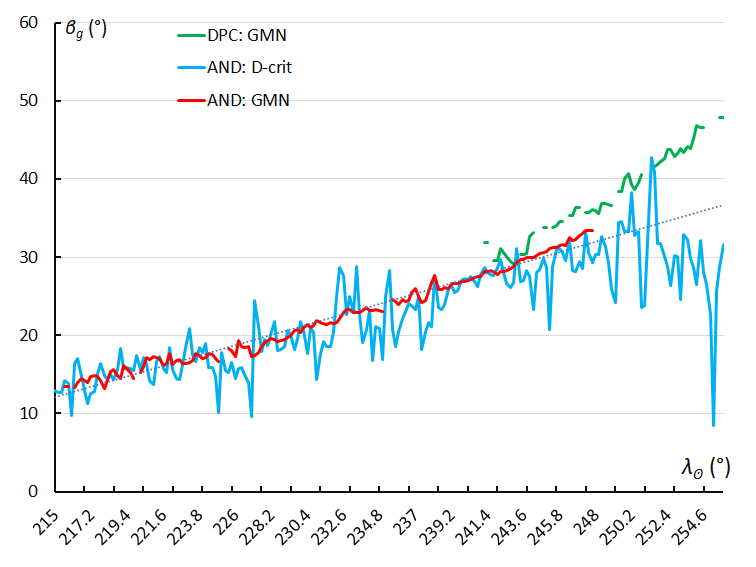
Figure 14 – The radiant drift in geocentric ecliptic latitude, using the sliding mean of the geocentric ecliptic latitude computed for a time interval of 0.4° in solar longitude in steps of 0.2°. The GMN shower identification is marked in red for the Andromedids and in green for the December psi Cassiopeiids, the Andromedids according to the orbit similarity identification are marked in blue.
The Andromedids are a very particular meteoroid stream with perturbed orbits in a way that it results in a mechanism compensating the usual radiant drift caused by the Earth’s movement around the Sun. The degree that these orbits have been smeared out during the transit of the Earth is very well reflected in a drift of the Sun-centered geocentric ecliptic coordinates. Most meteor showers do not display anything like this. Figures 13 and 14 show this effect. The radiant drift due to the perturbed smeared out orbits in Sun-centered geocentric ecliptic coordinates equals Δ(λ – λʘ) = –0.1°and Δβ = +0.12°. The drift in geocentric ecliptic latitude for the December psi Cassiopeiids deviates slightly in ecliptic latitude as can be seen in Figure 14. The authors have no explanation for this remarkable anomaly.
Apart of the radiant position which indicates the direction from where the particles hit the planet, the velocity relative to the Earth is another very important property of a meteor shower. Measuring the velocity of a fast-moving object on a short trail at the sky introduces instrumental measurement errors. If all shower meteors would have the same velocity, we should see a nice symmetric Gaussian distribution representing the spread caused by measurement errors. This is not the case whether we look at the Andromedids identified by GMN (Figure 15) or identified by the orbit similarity method (Figure 16). The GMN identification has very little dispersed orbits, while the orbit similarity method picks up more dispersed particles.
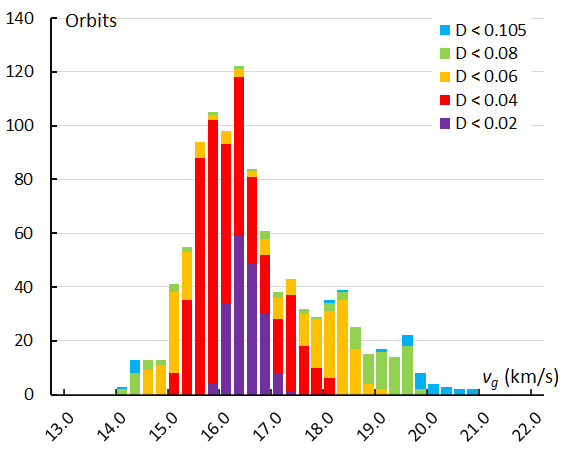
Figure 15 – The histogram with the distribution of the geocentric velocity obtained for Andromedids identified by the GMN shower identification method.
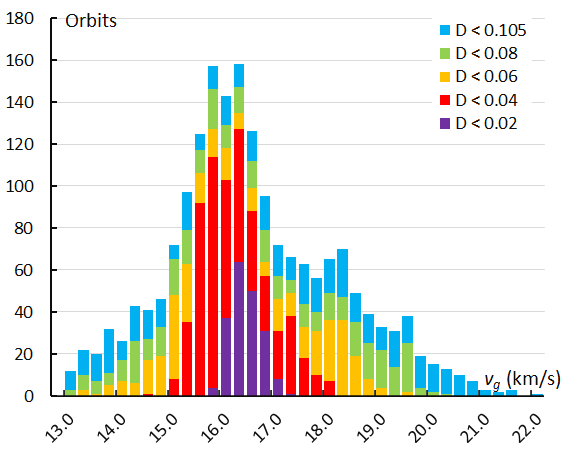
Figure 16 – The histogram with the distribution of the geocentric velocity obtained for Andromedids identified by the orbit similarity shower identification method.
The profiles appear skew and show different peaks, suggesting that some components with slightly different geocentric velocity contributed to the 2021 Andromedid activity. The different classes of similarity show a concentration of almost identical orbits (DD < 0.02) at vg = 16.3 km/s which is the geocentric velocity of the reference orbit obtained as mean orbit for all GMN identified Andromedids. The orbits with DD < 0.04 which correspond mainly with the orbits of the second and the last peak, had a slightly lower velocity. Several lower similarity orbits had a significant faster velocity compared to the main bulk of Andromedids. This requires a look at the variation in velocity in function of time, in our case we use the solar longitude λʘ.
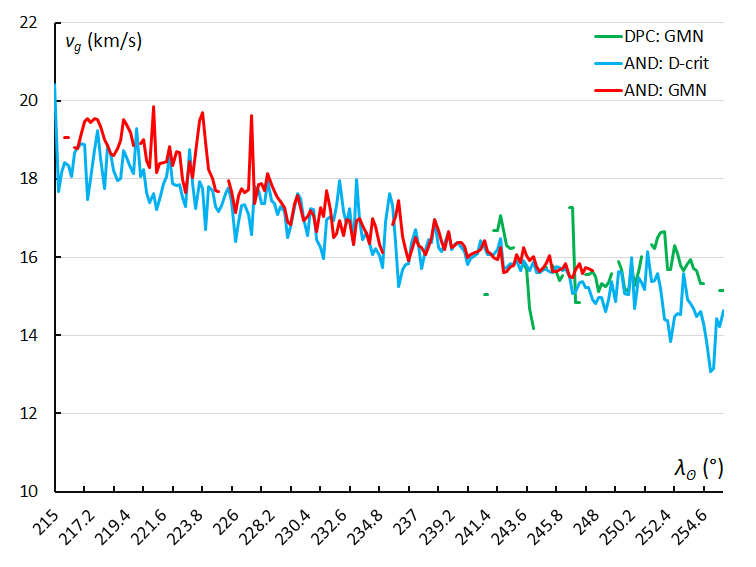
Figure 17 – The variation in geocentric velocity vg, using the sliding mean of the geocentric velocity computed for a time interval of 0.4° in solar longitude in steps of 0.2°. The GMN shower identification is marked in red for the Andromedids and in green for the December psi Cassiopeiids, the Andromedids according to the orbit similarity identification are marked in blue.
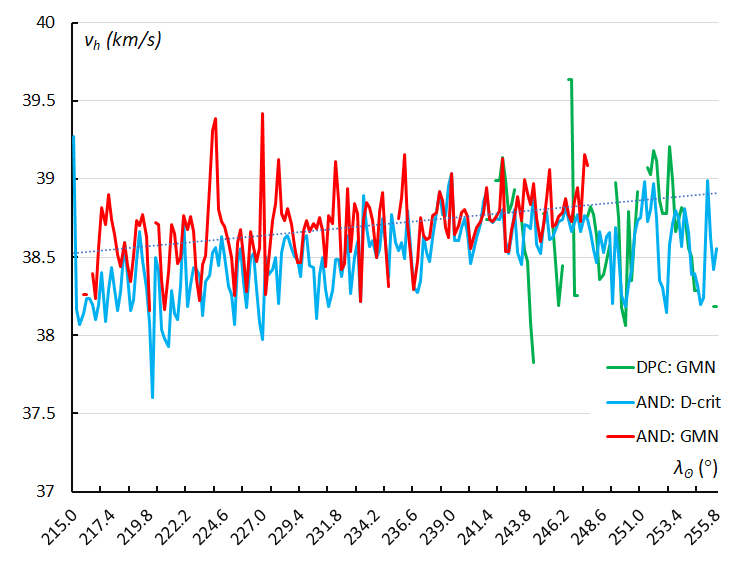
Figure 18 – The variation in heliocentric velocity vh, using the sliding mean of the heliocentric velocity computed for a time interval of 0.4° in solar longitude in steps of 0.2°. The GMN shower identification is marked in red for the Andromedids and in green for the December psi Cassiopeiids, the Andromedids according to the orbit similarity identification are marked in blue.
The change in geocentric velocity vg in function of the solar longitude is shown in Figure 17. The geocentric velocity is the result of the sum of the velocity vector of the Earth’s own movement around the Sun, about 29.8 km/s, and the velocity vector of the particle in its orbit around the Sun. The heliocentric velocity vh of the Andromedids appears to be constant, apart from a slight increase of 0.4 km/s between the start and then end of the activity period. The decrease in geocentric velocity is caused by the change in angle of entry of the Andromedids during the shower activity as the radiant moves towards the antapex. The different peaks in Figures 15 and 16 may be caused by the large input during the different peaks in the activity profile which appeared at different times with slightly different velocities.
Another interesting plot is the radiant distribution in Sun-centered geocentric ecliptic coordinates, color coded for the geocentric velocity (Figures 19 and 20). The Earth first encounters the fastest Andromedid particles and gradually intercepts Andromedid particles at lower geocentric velocity from more northern ecliptic latitudes and lower Sun-centered ecliptic longitude. Both shower identification methods show the same effect. The more scattered orbits defined by the orbit similarity method show the fastest Andromedids at higher Sun-centered ecliptic longitude at the beginning of the shower activity, the slowest particles appear towards the end of the activity.
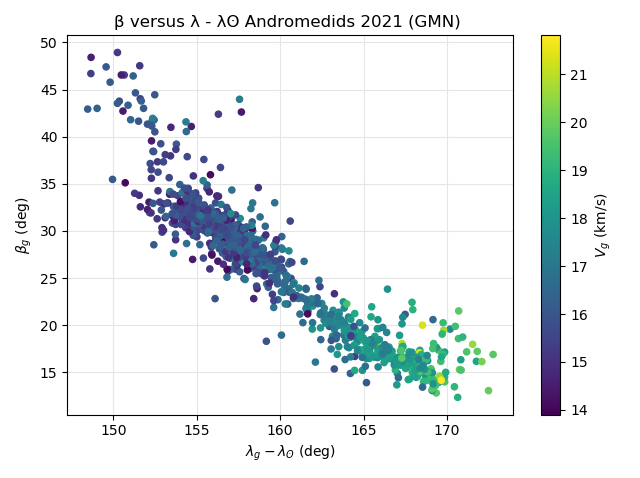
Figure 19 – The Andromedid radiants in Sun-centered geocentric ecliptic coordinates based on the GMN shower identification, color coded according to the geocentric velocity.
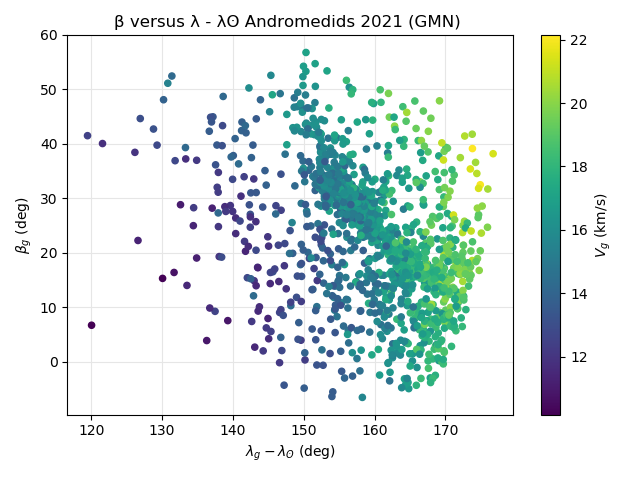
Figure 20 – The Andromedid radiants in Sun-centered geocentric ecliptic coordinates based on the orbit similarity shower identification, color coded according to the geocentric velocity.
The drifting in orbital elements
Longitude of perihelion Π
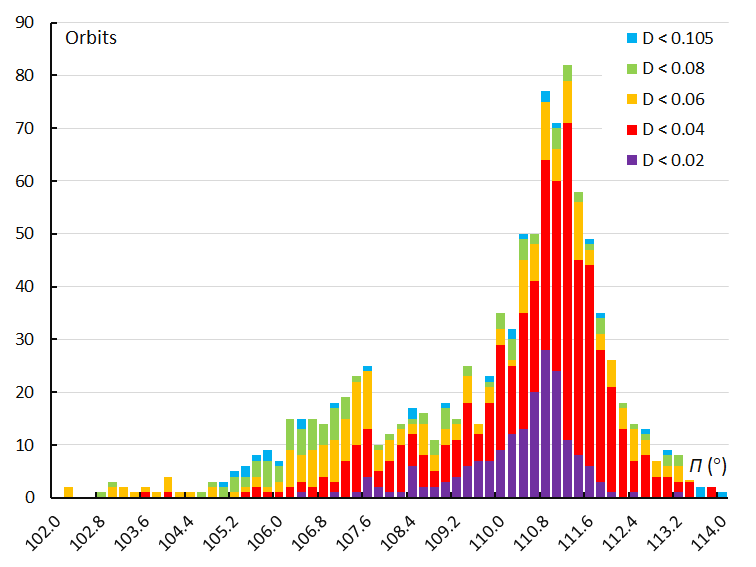
Figure 21 – The histogram with the distribution of the longitude of perihelion Π obtained for Andromedids identified by the GMN shower identification method.
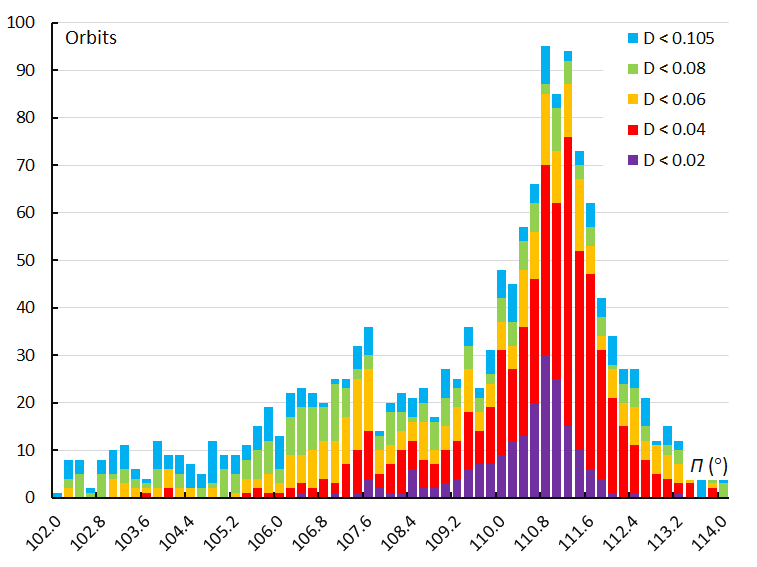
Figure 22 – The histogram with the distribution of the longitude of perihelion Π obtained for Andromedids identified by the orbit similarity shower identification method.
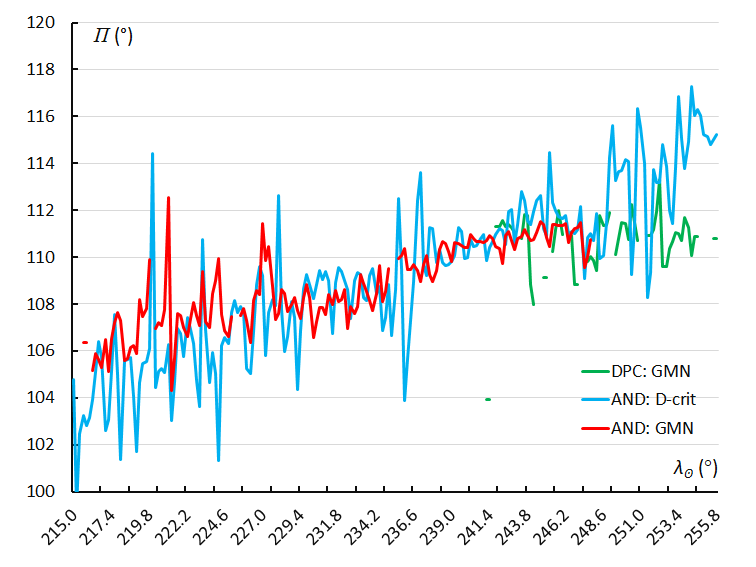
Figure 23 – The variation in longitude of perihelion Π, using the sliding mean of Π computed for a time interval of 0.4° in solar longitude in steps of 0.2°. The GMN shower identification is marked in red for the Andromedids and in green for the December psi Cassiopeiids, the Andromedids according to the orbit similarity identification are marked in blue.
The distribution of the longitude of perihelion Π, provides insight in the dispersion of the meteoroid stream at its perihelion which corresponds to its closest position to the Sun. The longitude of perihelion is composed by the time dependent longitude of the ascending node Ω and the argument of perihelion ω.
Both the GMN (Figure 21) and the orbit similarity shower identification (Figure 22) result in a similar asymmetric distribution with some peaks. The variation of the longitude of perihelion in function of the solar longitude λʘ indicates a slight increase for the Andromedids but remains rather constant for the December psi Cassiopeiids (Figure 23). The large scatter indicates that the positions of the perihelia of the Andromedids got very dispersed.
The inclination i
The inclination i provides insight in the orientation of the meteor orbits relative to the ecliptic. Both the GMN (Figure 24) and the orbit similarity shower identification (Figure 25) result in a similar asymmetric distribution with at least two distinct peaks.
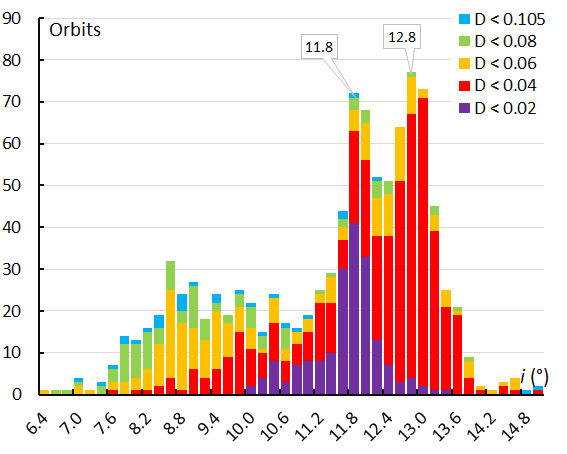
Figure 24 – The histogram with the distribution of the inclination i obtained for Andromedids identified by the GMN shower identification method.
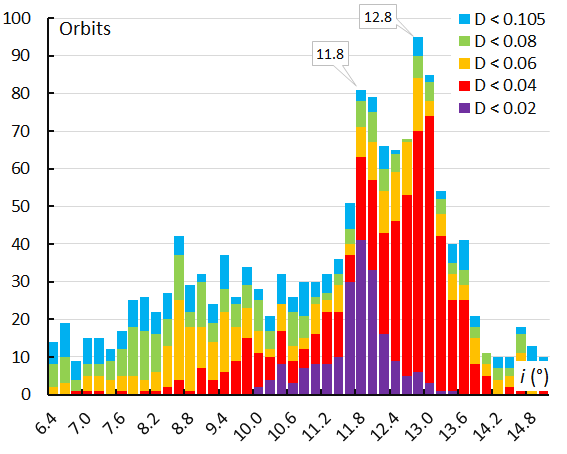
Figure 25 – The histogram with the distribution of the inclination i obtained for Andromedids identified by the orbit similarity shower identification method.
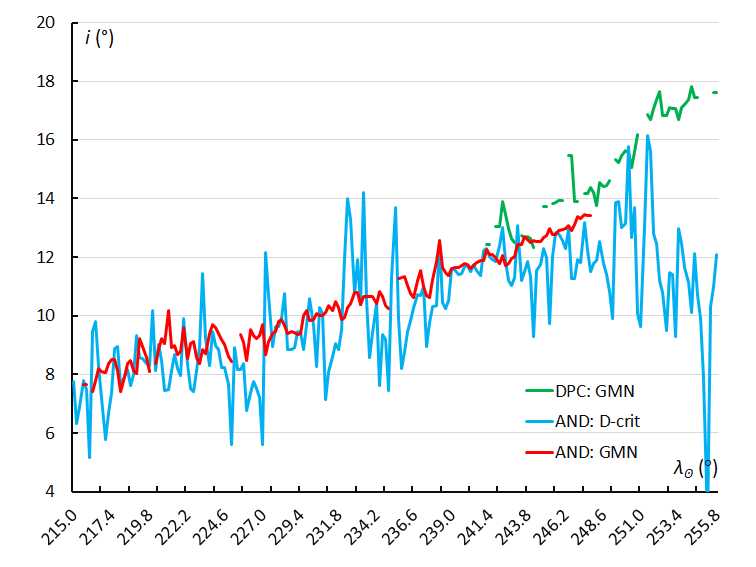
Figure 26 – The variation in inclination i, using the sliding mean of the inclination computed for a time interval of 0.4° in solar longitude in steps of 0.2°. The GMN shower identification is marked in red for the Andromedids and in green for the December psi Cassiopeiids, the Andromedids according to the orbit similarity identification are marked in blue.
Figure 26 shows that the wide range in inclination shown in Figures 24 and 25, changes in time. The first Andromedids encountered by Earth have a lower inclination than during the activity maxima. The peaks in the histogram correspond to the maxima in the activity profile. The gradual increase in inclination during the activity is obvious for the Andromedids and the December psi Cassiopeiids identified by GMN. The scatter at the end of the activity period for the orbit similarity identification is due to some outliers among fewer datapoints.
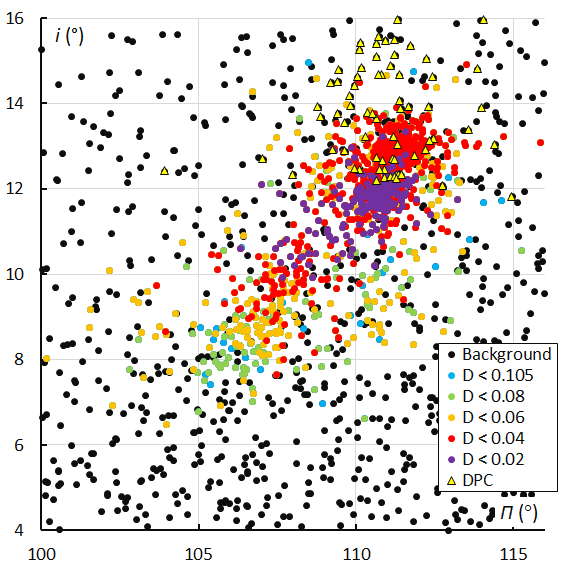
Figure 27 – The Andromedid orbits plotted as inclination i against the longitude of perihelion Π based on the GMN shower identification, color coded according to the orbit similarity criteria. The triangles indicate the Andromedids which were identified as December psi Cassiopeiids.
The inclination i can be plotted against the longitude of perihelion Π to check for concentrations within the meteoroid stream. The graph with the inclination i plotted against the longitude of perihelion Π shows two concentrations with the first modest peak at λʘ = 234° containing lower inclination orbits around Π = 107.6° with i = 10.6°. The two other peaks at λʘ = 239.4° and λʘ = 246.0° include higher inclination orbits at Π = 110.8° with i = 11.8° and at Π = 111.2° with i = 12.8°. The December psi Cassiopeiids at the end of the Andromedid activity appear with higher inclination and more dispersed in length of perihelion. The same picture appears in the plot with the GMN shower identification (Figure 27) as well as in the orbit similarity shower identification (Figure 28).
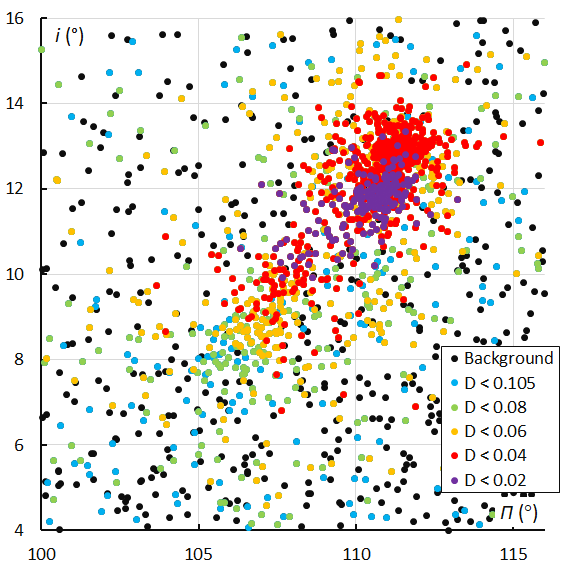
Figure 28 – The Andromedid orbits plotted as inclination i against the longitude of perihelion Π based on the orbit similarity shower identification, color coded according to the orbit similarity criteria. The December psi Cassiopeiids (DPC#446) orbits from Figure 27 are detected as Andromedids.
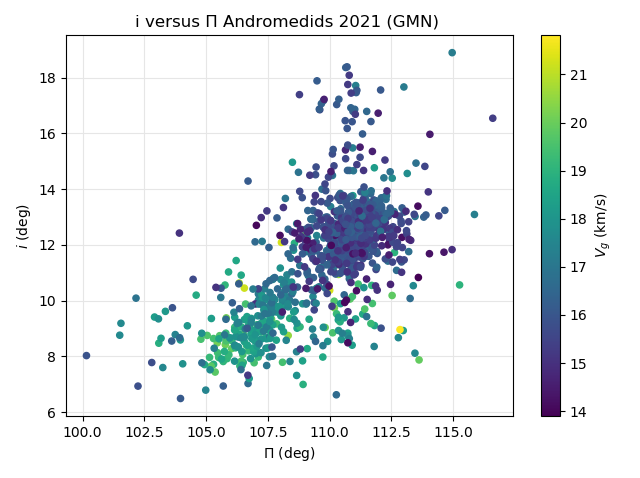
Figure 29 – The Andromedid orbits plotted as inclination i against the longitude of perihelion Π based on the GMN shower identification, color coded according to the geocentric velocity.
Looking at the distribution of the inclination against the longitude of perihelion color coded for the geocentric velocity, we see a concentration with at Π = 107.6° at about 9° inclination with mainly fast Andromedids. Another concentration appears at Π = 111° with an inclination of about 13° with significant slower Andromedids. The more scattered dots at higher inclinations were all identified as December psi Cassiopeiids (see Figure 27).
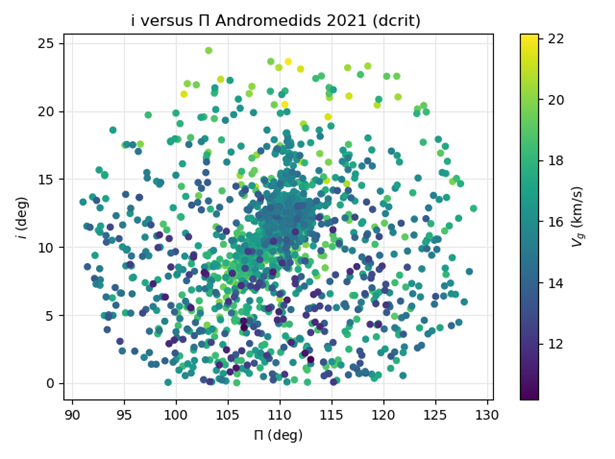
Figure 30 – The Andromedid orbits plotted as inclination i against the longitude of perihelion Π based on the orbit similarity shower identification, color coded according to the geocentric velocity.
The same plot for the orbit similarity shower identification shows a much larger scatter in inclination and longitude of perihelion (Figure 30). The two concentrations seen in Figure 29 are still visible but less distinct.
The perihelion distance q
The perihelion distance gives insight in the dispersion in the closest approach to the Sun of meteoroid orbits. The closer the particles of a meteoroid stream get to the Sun, the more intense their exposure to the destructive forces of the Sun. For the fragile cometary dust of comet 3D/Biela these particles will suffer a significant stress at each perihelion passage. If the distance to the Sun differs a lot for different components of the shower, this effect will have a different result for these components.
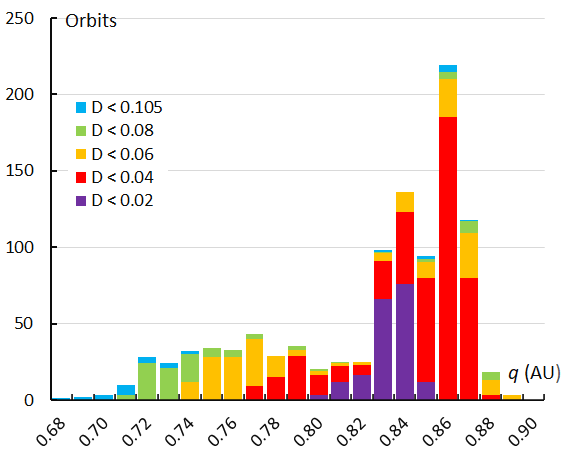
Figure 31 – The histogram with the distribution of the perihelion distance q obtained for Andromedids identified by the GMN shower identification method.
Looking at the histogram with the perihelion distance distribution we see a very asymmetric distribution covering a wide range of perihelion distances q with at least two distinct peaks at q = 0.84 A.U. and q = 0.86 A.U. Within a wide range from about 0.68 to almost 1.00 A.U. the registered Andromedid orbits undergo a significant different thermal stress at their perihelion passage. Both shower identification methods result in a similar histogram (Figures 31 and 32), with the orbit similarity method having more Andromedids at the beginning and the end of the activity period.
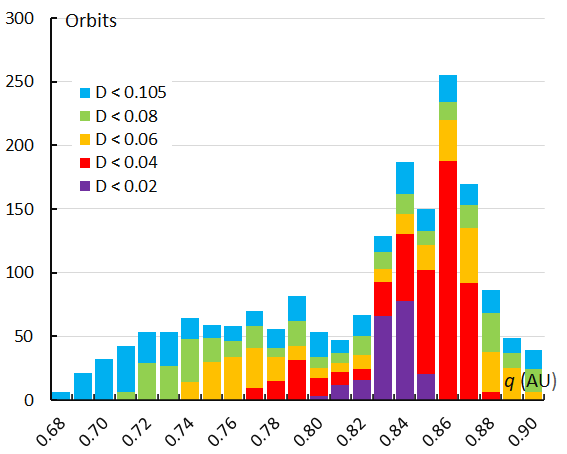
Figure 32 – The histogram with the distribution of the perihelion distance q obtained for Andromedids identified by the orbit similarity shower identification method.
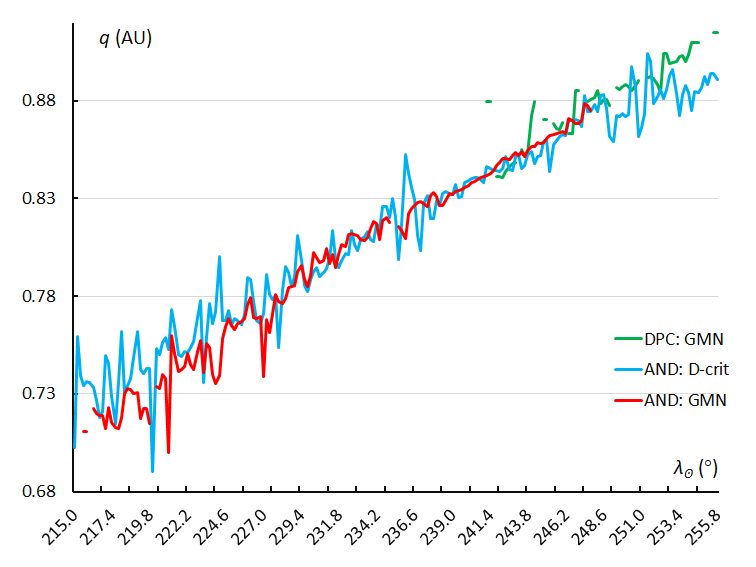
Figure 33 – The variation in perihelion distance q, using the sliding mean of the perihelion distance computed for a time interval of 0.4° in solar longitude in steps of 0.2°. The GMN shower identification is marked in red for the Andromedids and in green for the December psi Cassiopeiids, the Andromedids according to the orbit similarity identification are marked in blue.
Looking at the perihelion distance q in function of the solar longitude λʘ, a very distinct trend can be seen (Figure 33). The Andromedid activity starts with orbits with a perihelion distance closer to the Sun, gradually increasing the perihelion distance towards the Earth’s orbit during the Andromedid activity period. The December psi Cassiopeiids are perfectly in line with this trend. The peaks in Figures 31 and 32 correspond to the different maxima in the activity profile (Figures 1 and 2). The drift in perihelion distance during the transit of Earth through the stream is remarkable. The distribution of the perihelion distance in function of the longitude of perihelion and inclination provides some more insight in the structure of the stream.
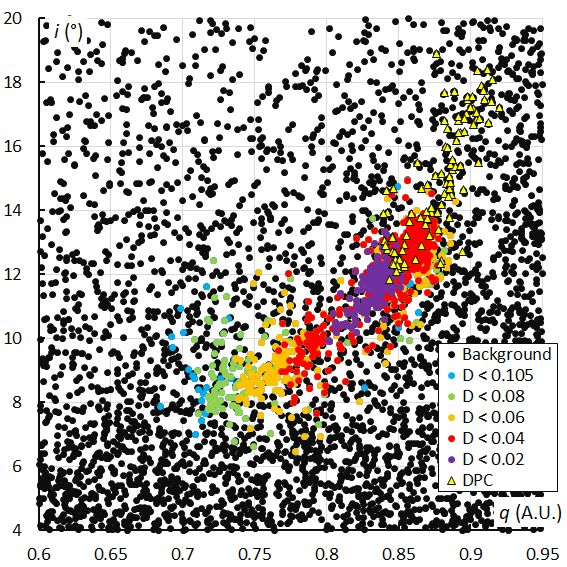
Figure 34 – The Andromedid orbits plotted as inclination i against the perihelion distance q based on the GMN shower identification, color coded according to the orbit similarity criteria. The triangles indicate the Andromedids which were identified as December psi Cassiopeiids.
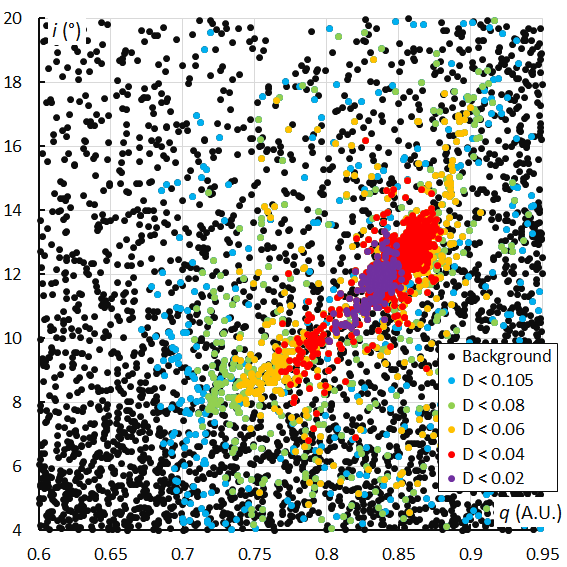
Figure 35 – The Andromedid orbits plotted as inclination i against the perihelion distance q based on the orbit similarity shower identification, color coded according to the orbit similarity criteria.
How does the inclination i, or the orientation of the Andromedid orbits relative to the ecliptic change with the perihelion distance q? Figure 34 shows a clear trend with an increasing perihelion distance and increasing inclination. Figures 26 and 33 show how the inclination and perihelion distance increase in function of the solar longitude. The plot based on the orbit similarity shower identification (Figure 35) displays more scatter but confirms the pattern of Figure 34.
Taking the geocentric velocity vg into account the fastest Andromedids appear at the lowest perihelion distances and lower inclination at the beginning of the activity period (Figure 36). The plot for the orbit similarity shower identification confirms this trend but appears more diffuse covering a wider range in inclination with mainly dispersed particles (Figure 37).
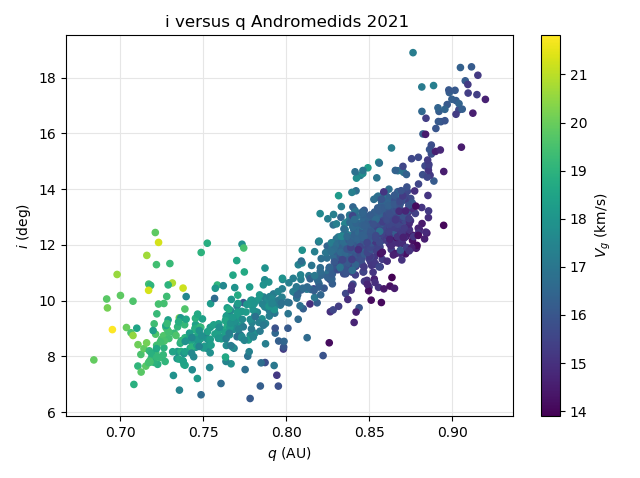
Figure 36 – The Andromedid orbits plotted as inclination i against the perihelion distance q based on the GMN shower identification, color coded according to the geocentric velocity.
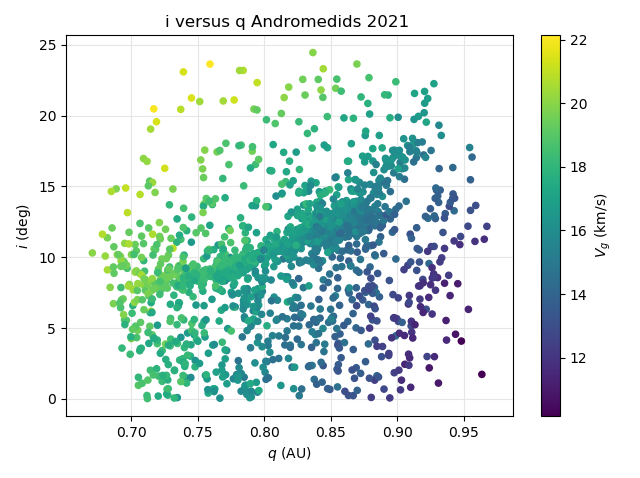
Figure 37 – The Andromedid orbits plotted as inclination i against the perihelion distance q based on the orbit similarity shower identification, color coded according to the geocentric velocity.
Looking at the distribution of the perihelion distance against the longitude of perihelion, we get a very good picture of the dispersion of the Andromedids at their perihelion in both longitude and distance to the Sun. Figure 38 shows this distribution where the first part of the activity period with the first moderate maximum appears separated from the dense concentration caused by the second and the third peak. The December psi Cassiopeiids partly overlap with the last concentration. The plot for the orbit similarity shower identification (Figure 39) confirms this picture, although with a larger spread in longitude of perihelion.
Taking the geocentric velocity vg into account, there is a clear trend with faster Andromedids at lower perihelion distances and slower meteors at higher perihelion distance (Figure 40). The orbit similarity shower identification results in the same picture but with larger scatter in longitude or perihelion (Figure 41).
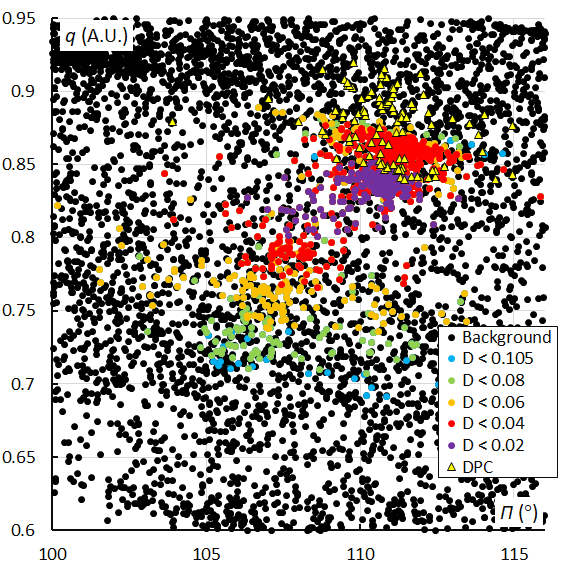
Figure 38 – The Andromedid orbits plotted as perihelion distance q against longitude of perihelion Π based on the GMN shower identification, color coded according to the orbit similarity criteria. The triangles indicate the Andromedids which were identified as December psi Cassiopeiids.
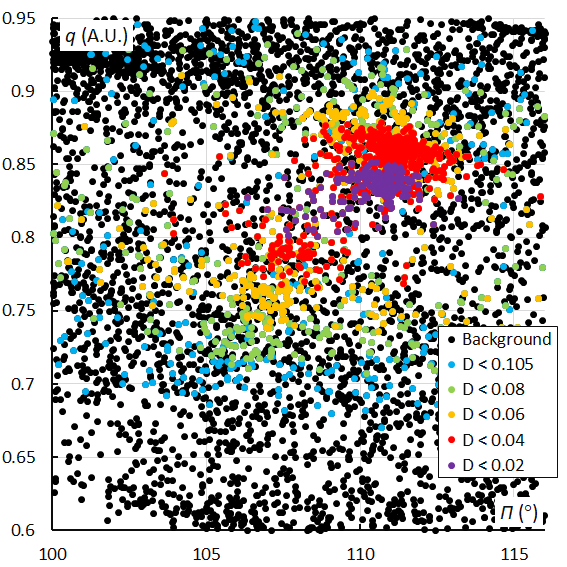
Figure 39 – The Andromedid orbits plotted as perihelion distance q against longitude of perihelion Π based on the orbit similarity shower identification, color coded according to the orbit similarity criteria.
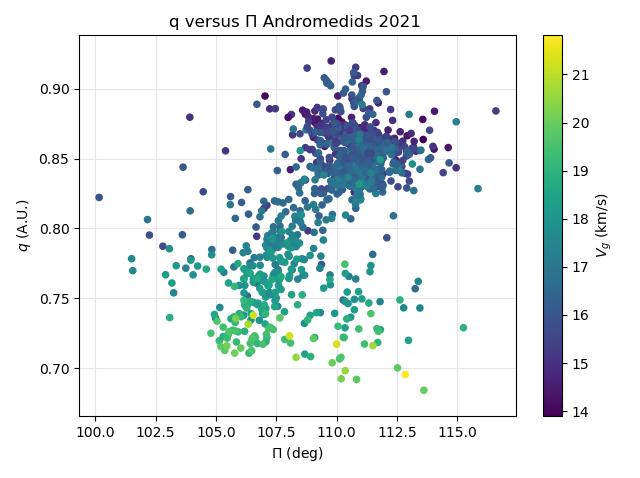
Figure 40 – The Andromedid orbits plotted as perihelion distance q against the longitude of perihelion Π based on the GMN shower identification, color coded according to the geocentric velocity.
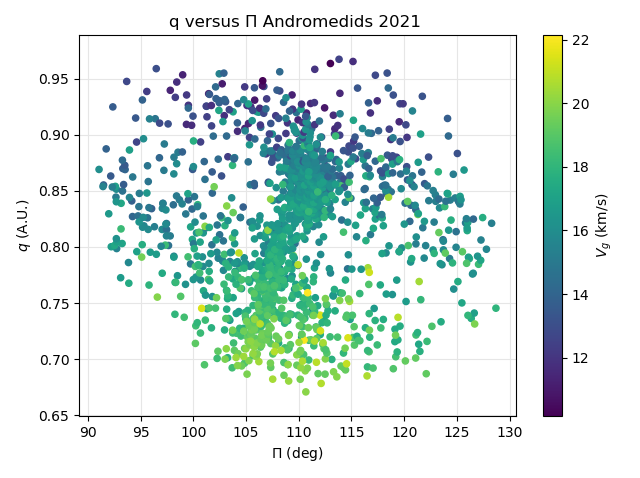
Figure 41 – The Andromedid orbits plotted as perihelion distance q against the longitude of perihelion Π based on the orbit similarity shower identification, color coded according to the geocentric velocity.
The eccentricity e
The eccentricity describes the shape of the orbit, with e = 0 for a perfect circle, e = 1 for a parabolic orbit and e > 1 for a hyperbolic orbit. The histogram for the eccentricities recorded for the Andromedids shows a slightly skew profile (Figures 42 and 43) for both shower identification methods.
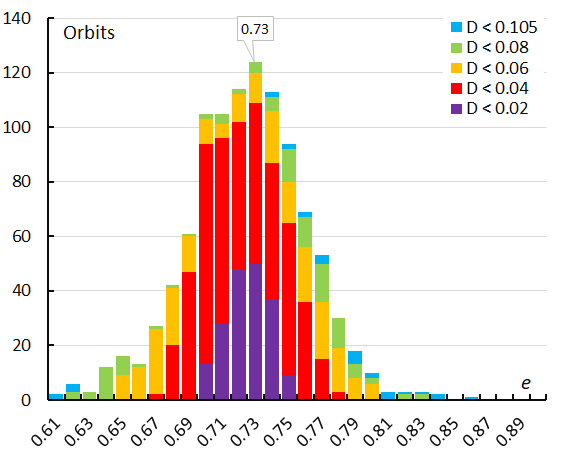
Figure 42 – The histogram with the distribution of the eccentricity e obtained for Andromedids identified by the GMN shower identification method.
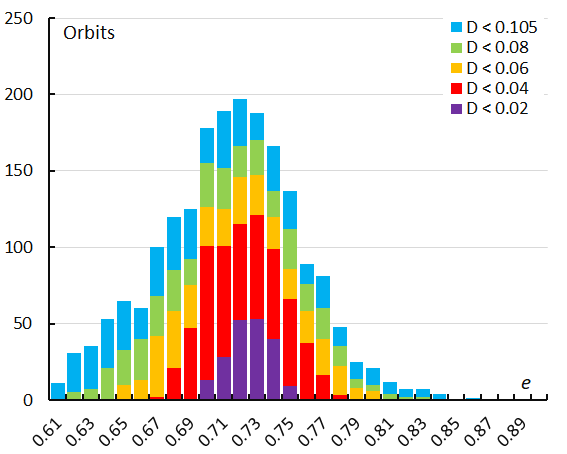
Figure 43 – The histogram with the distribution of the eccentricity e obtained for Andromedids identified by the orbit similarity shower identification method.
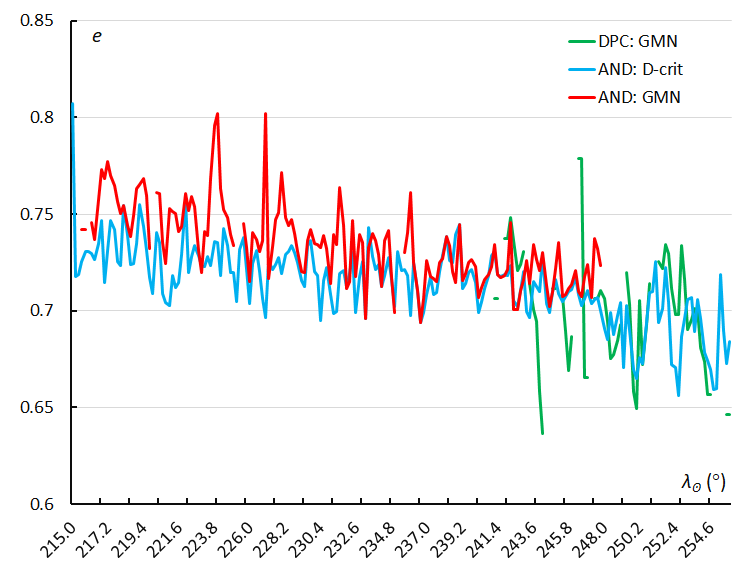
Figure 44 – The variation in eccentricity e, using the sliding mean of the eccentricity computed for a time interval of 0.4° in solar longitude in steps of 0.2°. The GMN shower identification is marked in red for the Andromedids and in green for the December psi Cassiopeiids, the Andromedids according to the orbit similarity identification are marked in blue.
Figure 44 presents the evolution of the eccentricity with time (solar longitude) and shows a slight decrease within a significant scatter during the activity period. The December psi Cassiopeiids fit in very well at the end of the activity period of the Andromedids.
The plot of the eccentricity against the longitude of perihelion (Figures 45 and 46) reveals a distinct concentration with the early orbits at higher eccentricity values and lower longitude of perihelion values. The second and third peak appear at slightly lower eccentricity and higher longitude of perihelion.
A clearer picture emerges when we look at the same plot with eccentricity against longitude of perihelion with the velocity color coded. In Figure 47 shows two concentrations, one formed at the first peak with higher eccentricity and lower longitude of perihelion. The second and the third peak form another concentration with slightly lower eccentricity, higher longitude of perihelion and significant lower velocities. The same trend can be seen in Figure 48 although more diffuse due to the much more dispersed orbits. At the top of Figure 47 we see that 4 data points with high eccentricity are missing in Figure 48. This is because the orbit similarity shower identification rejects these 4 orbits which were identified as Andromedids by the GMN shower identification.
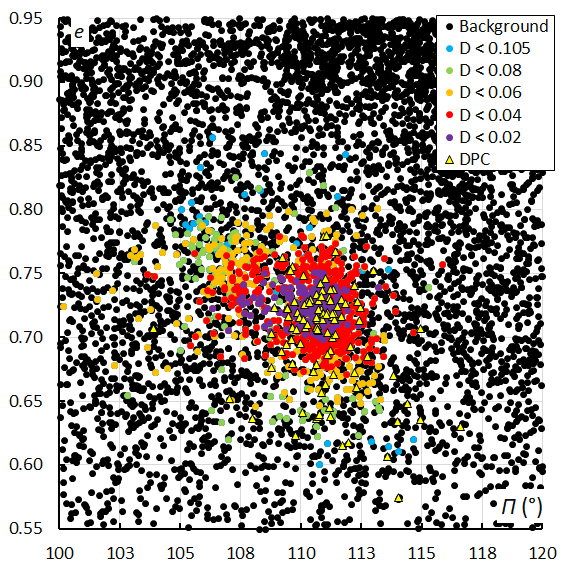
Figure 45 – The Andromedid orbits plotted as eccentricity e against longitude of perihelion Π based on the GMN shower identification, color coded according to the orbit similarity criteria. The triangles indicate the Andromedids which were identified as December psi Cassiopeiids.
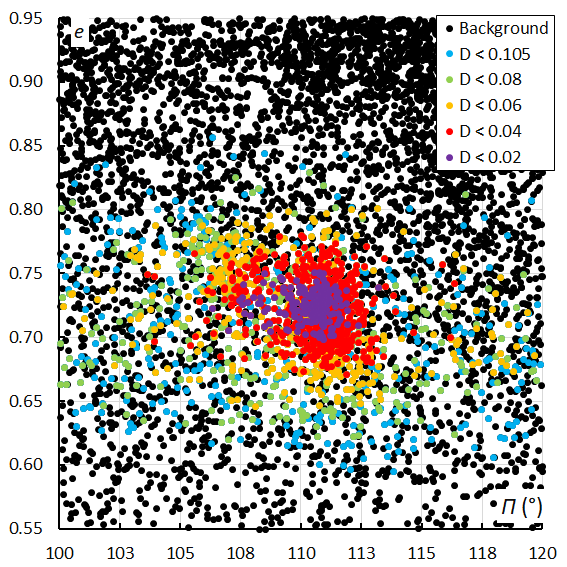
Figure 46 – The Andromedid orbits plotted as eccentricity e against longitude of perihelion Π based on the orbit similarity shower identification, color coded according to the orbit similarity criteria.
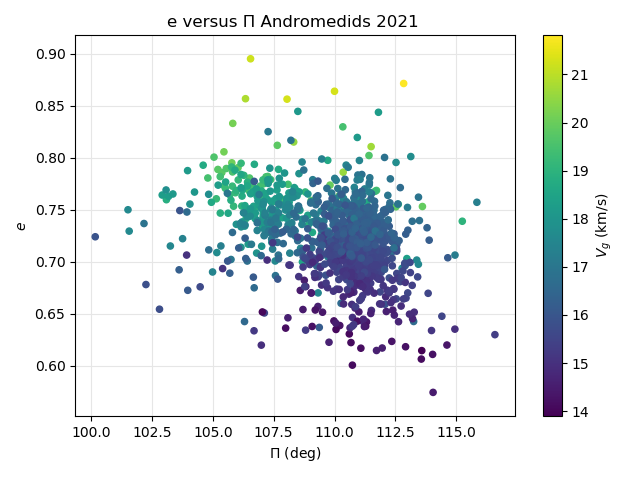
Figure 47 – The Andromedid orbits plotted as eccentricity e against the longitude of perihelion Π based on the GMN shower identification, color coded according to the geocentric velocity.
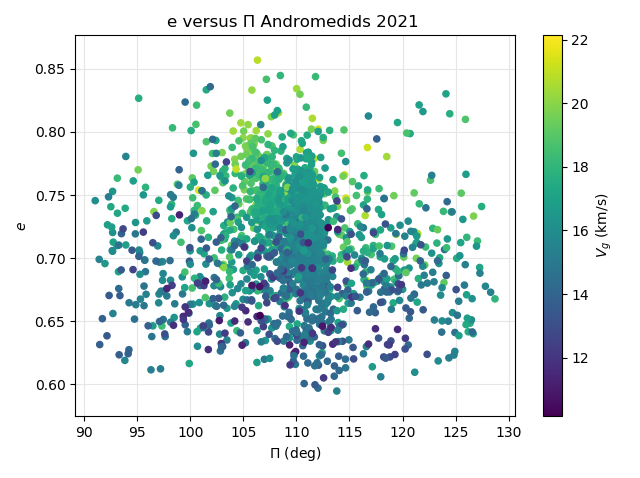
Figure 48 – The Andromedid orbits plotted as eccentricity e against the longitude of perihelion Π based on the orbit similarity shower identification, color coded according to geocentric velocity.
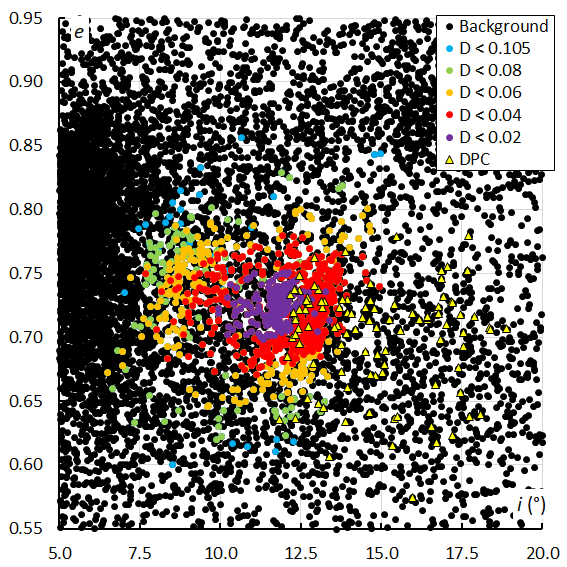
Figure 49 – The Andromedid orbits plotted as eccentricity e against the inclination i based on the GMN shower identification, color coded according to the orbit similarity criteria. The triangles indicate the Andromedids which were identified as December psi Cassiopeiids.
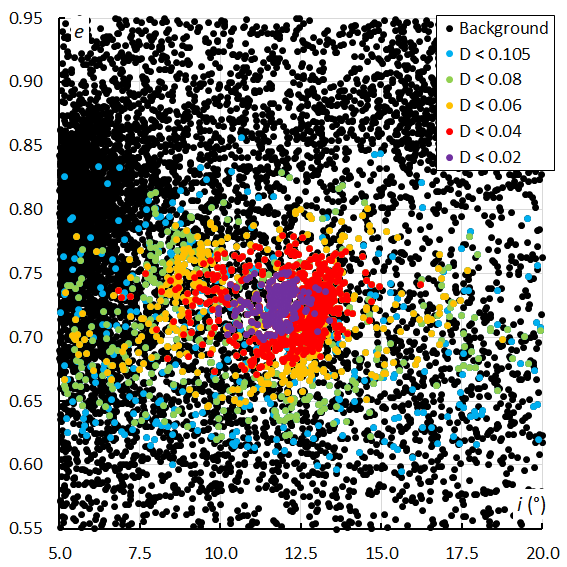
Figure 50 – The Andromedid orbits plotted as eccentricity e against the inclination i based on the orbit similarity shower identification, color coded according to the orbit similarity criteria.
The plot of the eccentricity e against the inclination i shows a concentration with the first peak Andromedid orbits at higher eccentricities with lower inclination and the second and third maximum Andromedids with slightly lower eccentricity at higher inclinations (Figure 49). The December psi Cassiopeiids appear more dispersed mainly in inclination. The plot with the orbit similarity shower identification confirms the same trend, although many more dispersed orbits, including the December psi Cassiopeiids were identified as Andromedids (Figure 50).
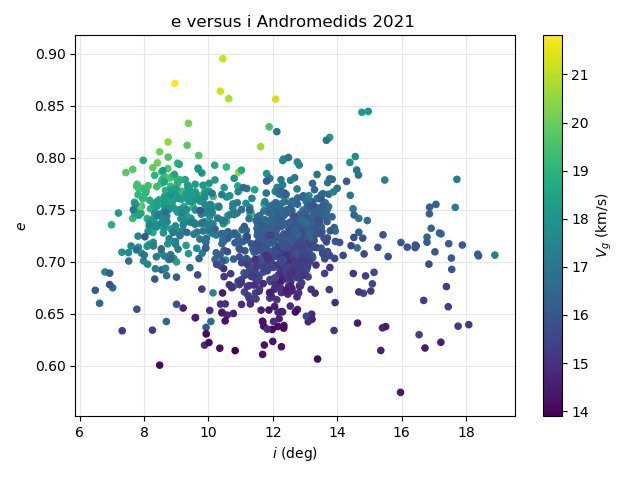
Figure 51 – The Andromedid orbits plotted as eccentricity e against the inclination i based on the GMN shower identification, color coded according to the geocentric velocity.
The same plot but with the velocity color coded (Figure 51) shows two more distinct concentrations with faster Andromedids with higher eccentricity and lower inclination during the first weeks of the activity with the first peak. The second and third peak occurred at higher inclination with slightly lower eccentricity and with lower velocity. The plot based on the orbit similarity (Figure 52) confirms this trend, although with a larger dispersion in inclination. The lower the eccentricity and the lower the inclination, the slower the velocity. Four data points at high eccentricity in Figure 51 have disappeared in Figure 52 because the orbit similarity criteria rejected these orbits which were identified as Andromedids by GMN.
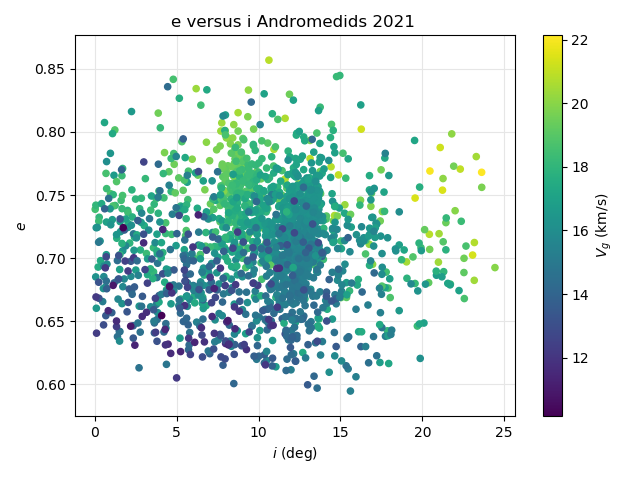
Figure 52 – The Andromedid orbits plotted as eccentricity e against the inclination i based on the orbit similarity shower identification, color coded according to the geocentric velocity.
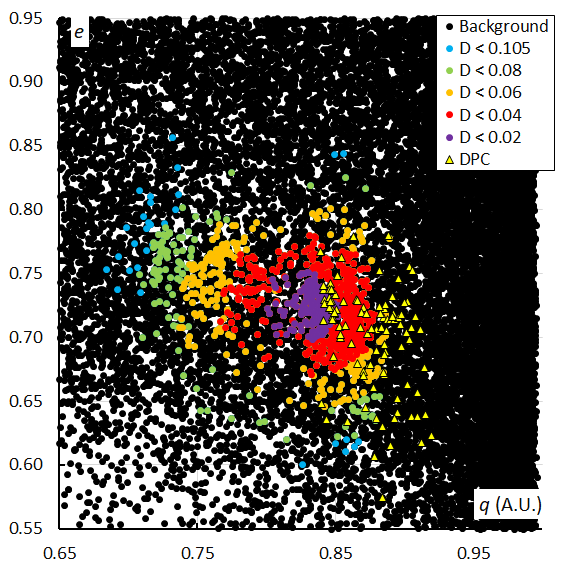
Figure 53 – The Andromedid orbits plotted as eccentricity e against the perihelion distance q based on the GMN shower identification, color coded according to the orbit similarity criteria. The triangles indicate the Andromedids which were identified as December psi Cassiopeiids.
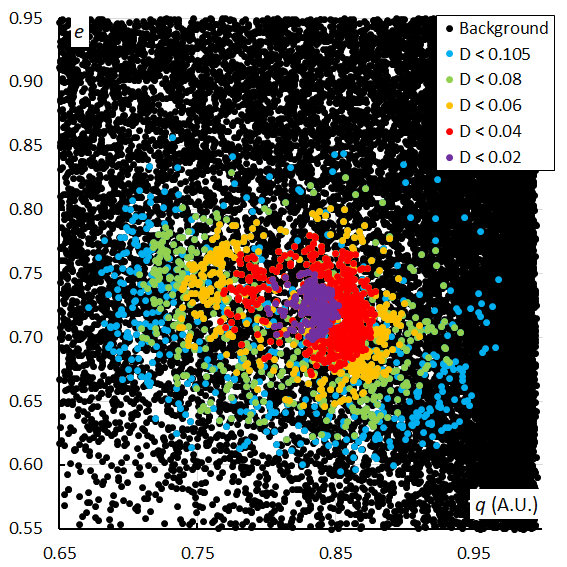
Figure 54 – The Andromedid orbits plotted as eccentricity e against the perihelion distance q based on the orbit similarity shower identification, color coded according to the orbit similarity criteria.
Plotting the eccentricity e against the perihelion distance q, a similar picture emerges as for the inclination. A first concentration can be seen at higher eccentricity and smaller perihelion distance, including the first peak. The other concentration at larger perihelion distance covers the second and the third peaks. the December psi Cassiopeiids fit in this plot with some larger dispersion after the main Andromedid activity (Figure 53). The plot based on the orbit similarity shower identification (Figure 54) confirms this result with many more dispersed orbits identified as Andromedids.
The plot of eccentricity e against perihelion distance q, color coded for the velocity shows two distinct concentrations. The first concentration at smaller perihelion distances appears with the fastest Andromedids, the second concentration at larger perihelion distances at slightly lower eccentricity includes slower Andromedids (Figure 55).
The plot based on the orbit similarity shower identification displays a more diffuse picture, including more dispersed orbits. The higher the eccentricity and the smaller the perihelion distance, the faster the velocity, the larger the perihelion distance, the lower the eccentricity, the slower the velocity (Figure 56).
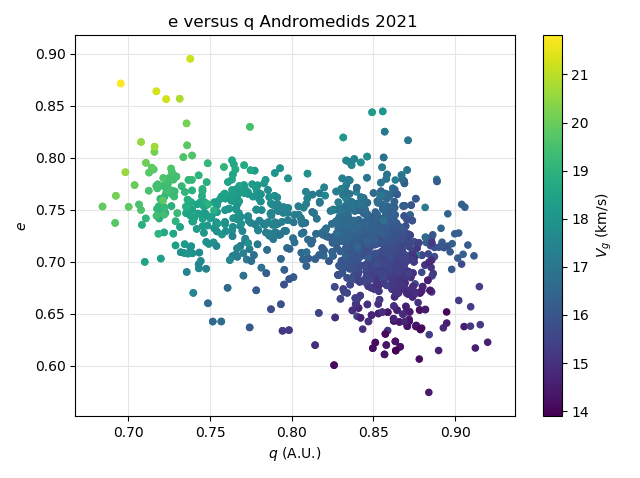
Figure 55 – The Andromedid orbits plotted as eccentricity e against the perihelion distance q based on the GMN shower identification, color coded according to the geocentric velocity.
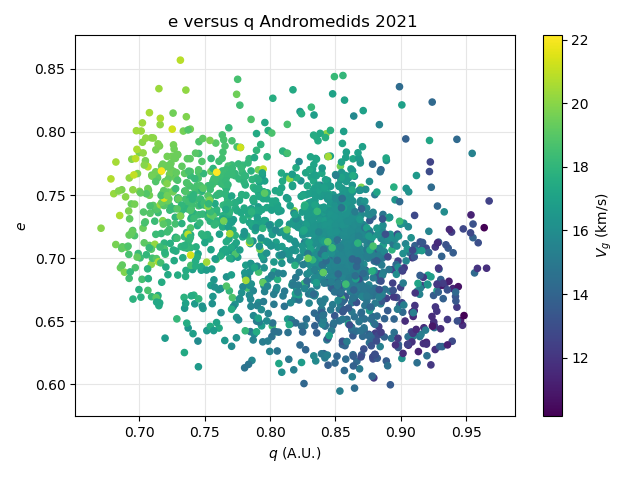
Figure 56 – The Andromedid orbits plotted as eccentricity e against the perihelion distance q based on the orbit similarity shower identification, color coded according to the geocentric velocity.
The semi major axis a
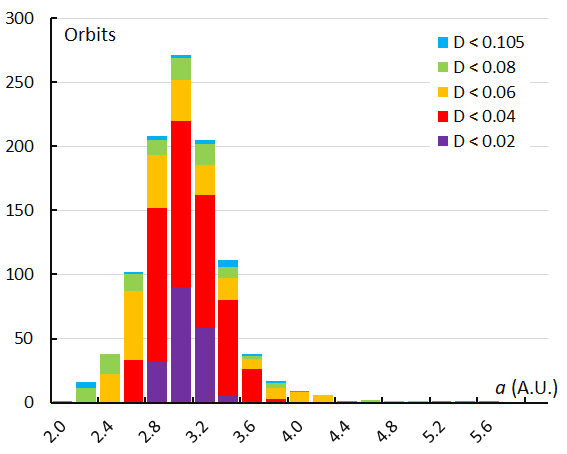
Figure 57 – The histogram with the distribution of the semi-major axis a obtained for Andromedids identified by the GMN shower identification method.
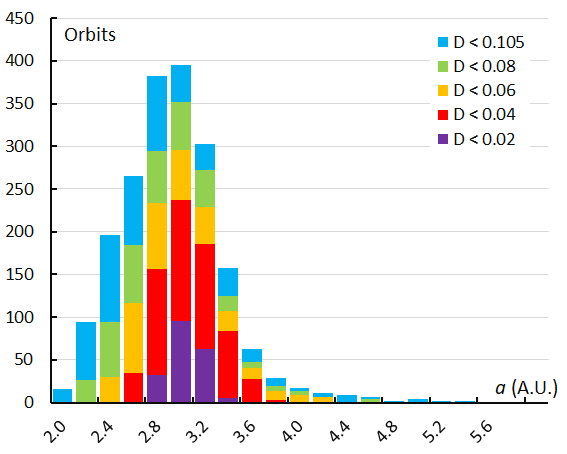
Figure 58 – The histogram with the distribution of the semi-major axis a obtained for Andromedids identified by the orbit similarity shower identification method.
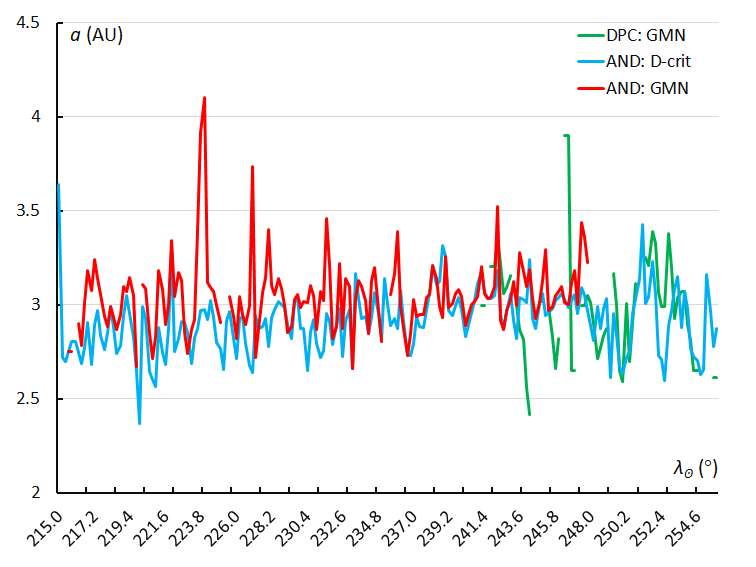
Figure 59 – The variation in semi-major axis a, using the sliding mean of the semi-major axis computed for a time interval of 0.4° in solar longitude in steps of 0.2°. The GMN shower identification is marked in red for the Andromedids and in green for the December psi Cassiopeiids, the Andromedids according to the orbit similarity identification are marked in blue.
The semi major axis is the easiest element to visualize for an elliptic orbit and can be calculated using the perihelion distance q and the eccentricity e as:
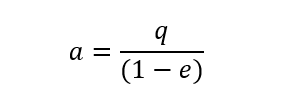
The semi-major axis is the most stable orbital element during the transit of Earth through the Andromedid stream, resulting in a symmetric profile in the histogram for both shower identification methods (Figures 57 and 58).
The values of the semi-major axis remain stable around 3.0 A.U. during the entire Andromedid activity (Figure 29) and the December psi Cassiopeiids fit very well in this graph.
Andromedid magnitude distribution
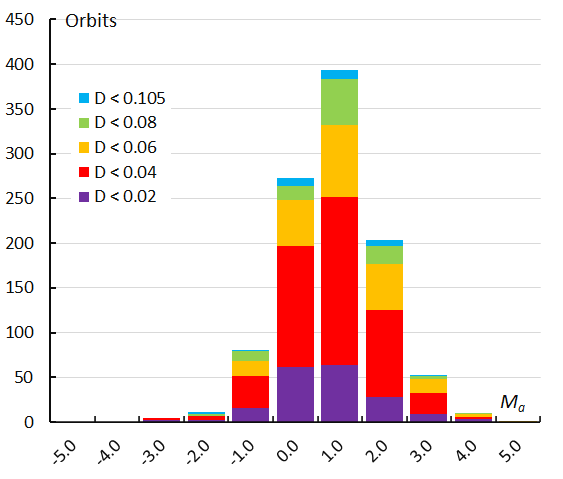
Figure 60 – The histogram with the distribution of the absolute magnitudes recorded for Andromedids identified by the GMN shower identification method.
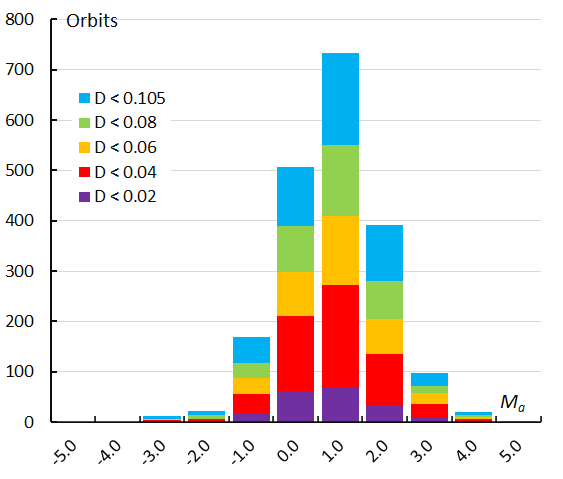
Figure 61 – The histogram with the distribution of the absolute magnitudes recorded for Andromedids identified by the orbit similarity shower identification method.
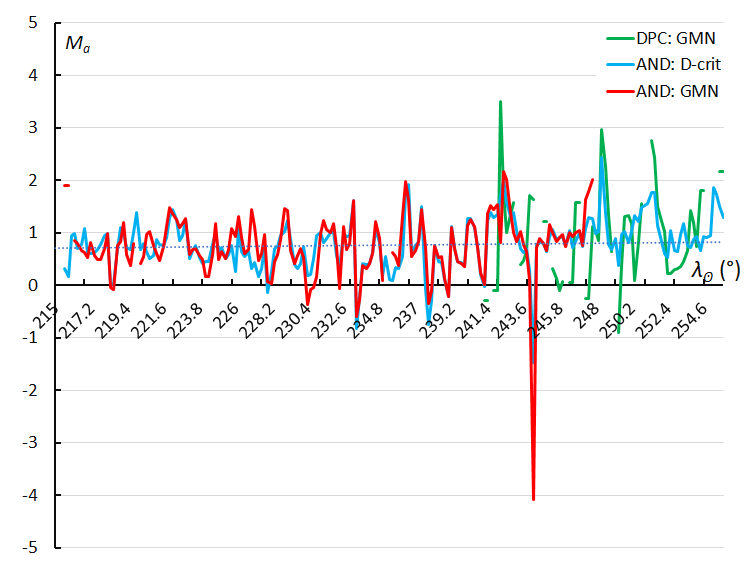
Figure 62 – The variation in absolute magnitude, using the sliding mean of the absolute magnitude computed for a time interval of 0.4° in solar longitude in steps of 0.2°. The GMN shower identification is marked in red for the Andromedids and in green for the December psi Cassiopeiids, the Andromedids according to the orbit similarity identification are marked in blue.
Looking at the magnitude distribution, based on the absolute magnitudes derived from the measured intensity of the video recordings, the available data indicate that the Andromedids were mainly faint meteors. Apart from some isolated fireballs rather few bright Andromedids were recorded. The orbit similarity method seems to identify mainly more fainter shower members than the GMN method (Figures 60 and 61).
Looking at the average absolute magnitude during the activity period no trend or variation can be detected apart from scatter caused by some outliers (Figure 62).
The complex composition of the shower
The unusual radiant drift and significant change in orbital elements during the activity period make it impossible to identify these orbits correctly with a single mean orbit as reference. The radiant drift cannot be determined with a simple linear fit because of the unusual composition of the Andromedid shower. Masahiro Koseki (2021) studied the annual activity of the Andromedids based on SonotaCo orbit data for the period 2007–2018 and found the same radiant drift in Sun-centered ecliptic coordinates and the same trend in the changing orbital elements.
Instead of using a single reference orbit to try to identify Andromedid orbits, it would be more appropriate to use a matrix of orbital elements to take the significant changes in the orbital elements into account. In an attempt to visualize the effect of the selection of the reference orbit on the identification of Andromedid orbits and the subsequent activity profile; the mean orbit has been calculated based on a reference orbit obtained for different time intervals.
The mean orbits (Jopek, 1993), obtained with reference orbits valid for different time intervals have been listed in Table 1. First 7 intervals were used between solar longitude 215° and 250° in steps of 5°. Three mean orbits were obtained for the three shower maxima intervals,
222.5°–228.5°, 238.5°–242.5° and 245.6°–246.1°.
Table 1 – The mean orbits for the Andromedids identified with a reference orbit calculated for a specific range of GMN-identified orbits.
| Range ref. | λʘ | αg | δg | λg–λʘ | βg | vg | a | q | e | i | Ω | ω | N |
| λʘ (°) | (°) | (°) | (°) | (°) | (°) | km/s | A.U. | A.U. | (°) | (°) | (°) | D < 0.04 | |
| 215–220 | 217.65 | 20.6 | 22.2 | 169.9 | 12.5 | 19.0 | 2.96 | 0.722 | 0.7555 | 8.4 | 218.22 | 248.43 | 221 |
| 220–225 | 222.57 | 22.0 | 25.3 | 167.4 | 14.9 | 18.3 | 3.00 | 0.749 | 0.7502 | 9.0 | 222.70 | 244.62 | 279 |
| 225–230 | 227.44 | 23.2 | 28.1 | 164.6 | 17.0 | 17.4 | 2.96 | 0.776 | 0.7376 | 9.5 | 227.48 | 240.65 | 295 |
| 230–235 | 232.21 | 23.7 | 32.4 | 162.1 | 20.8 | 16.9 | 3.01 | 0.807 | 0.7315 | 10.3 | 232.46 | 235.65 | 507 |
| 235–240 | 238.71 | 25.2 | 37.6 | 159.0 | 25.2 | 16.2 | 2.99 | 0.832 | 0.7216 | 11.6 | 238.90 | 231.36 | 754 |
| 240–245 | 242.55 | 25.7 | 41.4 | 157.3 | 28.5 | 15.9 | 2.98 | 0.849 | 0.7155 | 12.2 | 242.49 | 228.39 | 758 |
| 245–250 | 246.54 | 25.6 | 44.3 | 154.7 | 31.2 | 15.5 | 3.01 | 0.865 | 0.7129 | 13.0 | 246.00 | 225.26 | 739 |
| 222.5–228.5 | 225.25 | 22.6 | 27.1 | 166.0 | 16.3 | 17.8 | 2.94 | 0.772 | 0.7372 | 9.3 | 227.03 | 241.37 | 297 |
| 238.5–242.5 | 240.45 | 25.6 | 39.7 | 158.5 | 26.9 | 16.2 | 2.99 | 0.839 | 0.7191 | 11.8 | 240.38 | 230.24 | 758 |
| 245.6–246.1 | 245.84 | 25.8 | 44.6 | 155.5 | 31.4 | 15.7 | 3.00 | 0.864 | 0.7124 | 12.9 | 245.80 | 225.54 | 742 |
| DPC | 243.63 | 25.6 | 42.7 | 156.1 | 30.0 | 15.8 | 2.92 | 0.874 | 0.7009 | 14.77 | 248.39 | 222.52 | 656 |
The mean orbit for the December psi Cassiopeiids identified by the GMN shower identification method has been used as reference orbit too (DPC).
This study has been based on a single reference orbit used to identify Andromedids independently from the GMN shower identification. The mean orbit taken for the entire activity period is a compromise and may fail to identify Andromedids at the start and at the end of the activity period. Using a series of reference orbits based on different activity intervals, we can consider the activity profile according to these different reference orbits. The relevance of these reference orbits in Table 1 is given by the number of orbits that fulfil the high threshold similarity DD < 0.04 (Table 1). The resulting profiles are presented in Figures 63 to 73. The influence of the chosen reference orbit is obvious. The terms “peak” and “maximum” are very relative as these refer to activity levels of maximum 35% of the sporadic background activity.
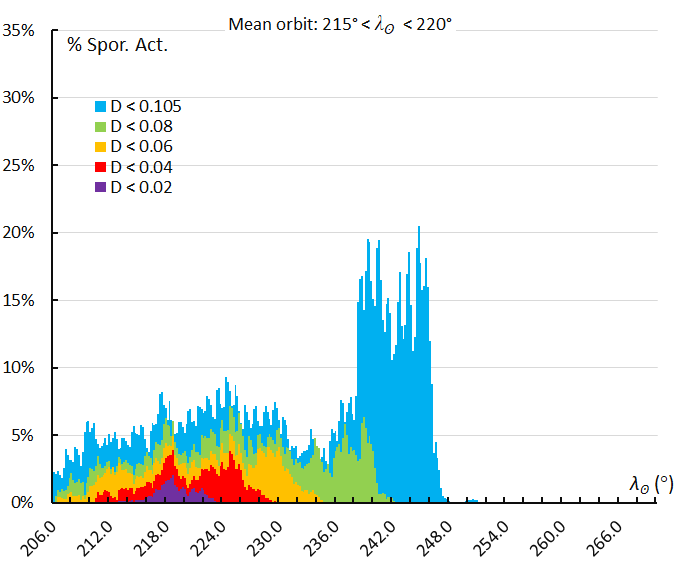
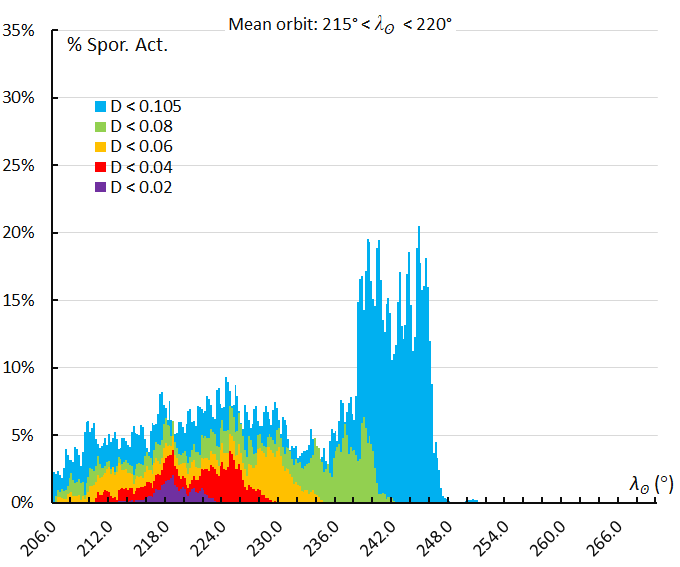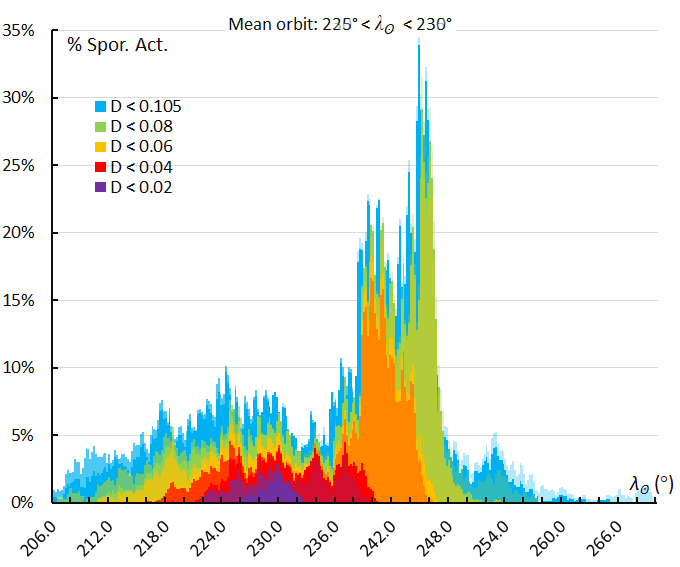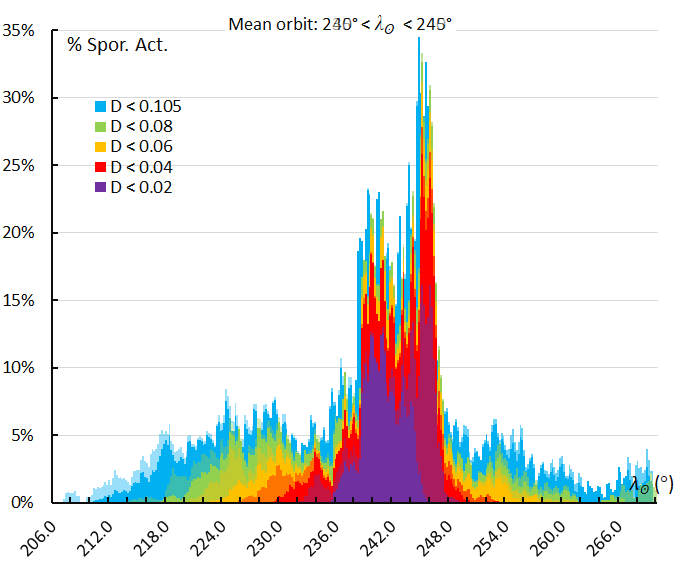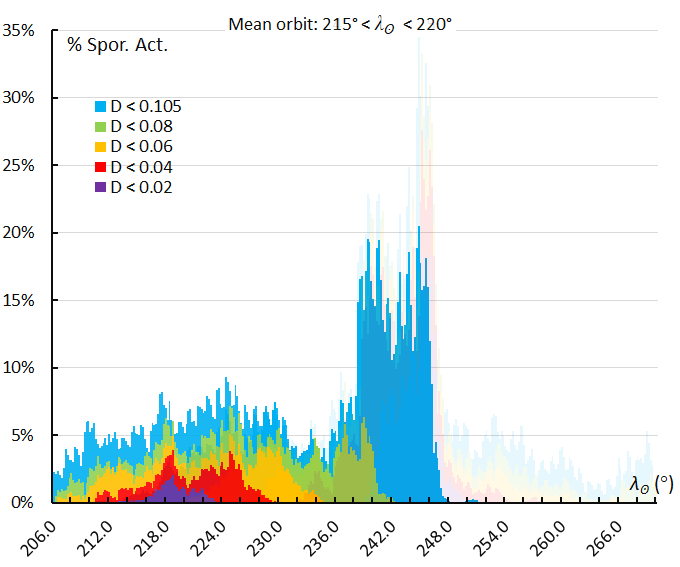
Figure 63 – The activity profile based on the orbit similarity shower identification using a reference orbit derived for the activity interval 215° < λʘ < 220°.
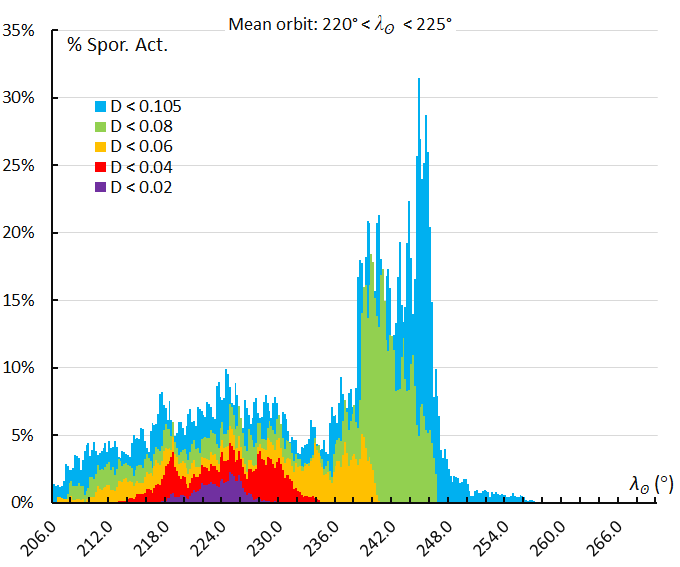
Figure 64 – The activity profile based on the orbit similarity shower identification using a reference orbit derived for the activity interval 220° < λʘ < 225°.
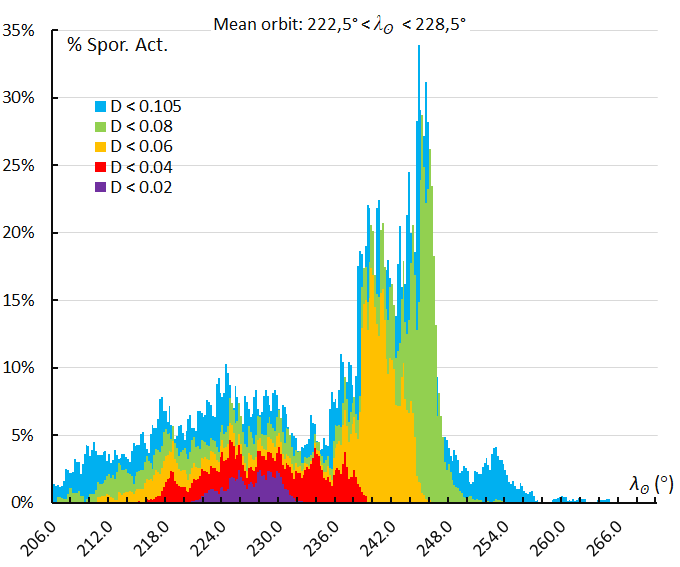
Figure 65 – The activity profile based on the orbit similarity shower identification using a reference orbit derived for the activity interval 222.5° < λʘ < 228.5°, the first maximum.
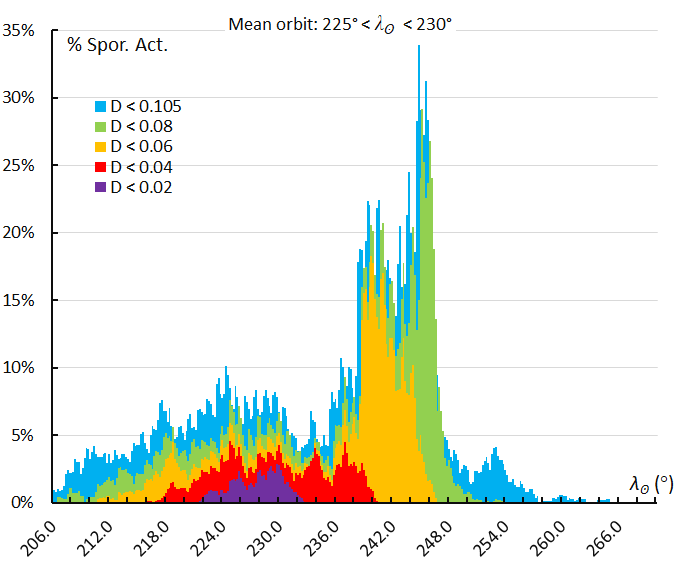
Figure 66 – The activity profile based on the orbit similarity shower identification using a reference orbit derived for the activity interval 225° < λʘ < 230°.
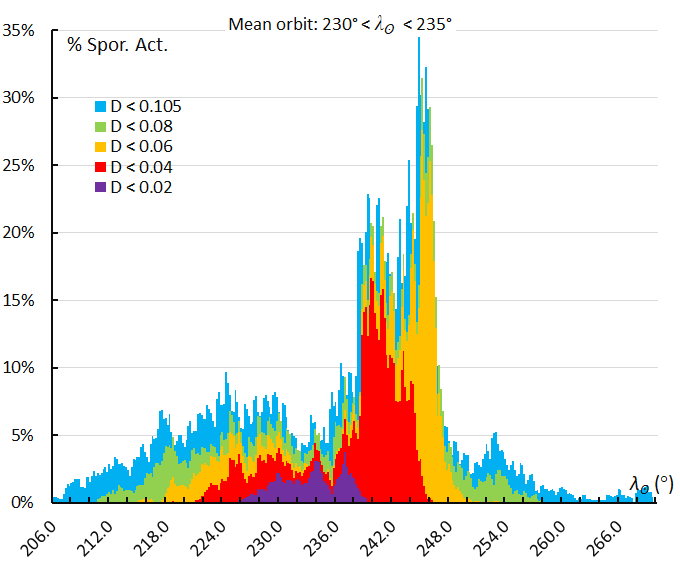
Figure 67 – The activity profile based on the orbit similarity shower identification using a reference orbit derived for the activity interval 230° < λʘ < 235°.
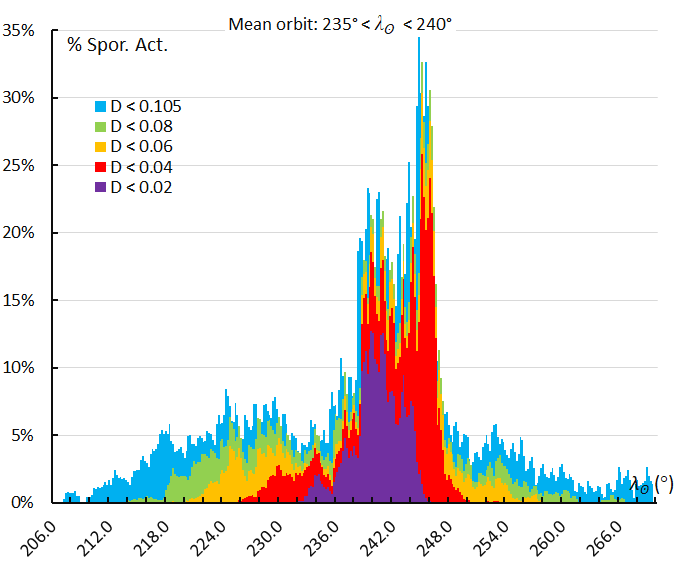
Figure 68 – The activity profile based on the orbit similarity shower identification using a reference orbit derived for the activity interval 235° < λʘ < 240°.
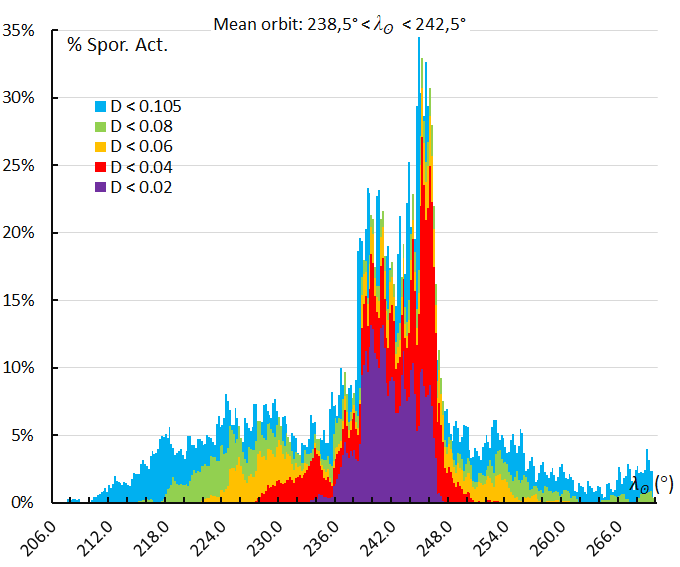
Figure 69 – The activity profile based on the orbit similarity shower identification using a reference orbit derived for the activity interval 238.5° < λʘ < 242.5°, the second maximum.
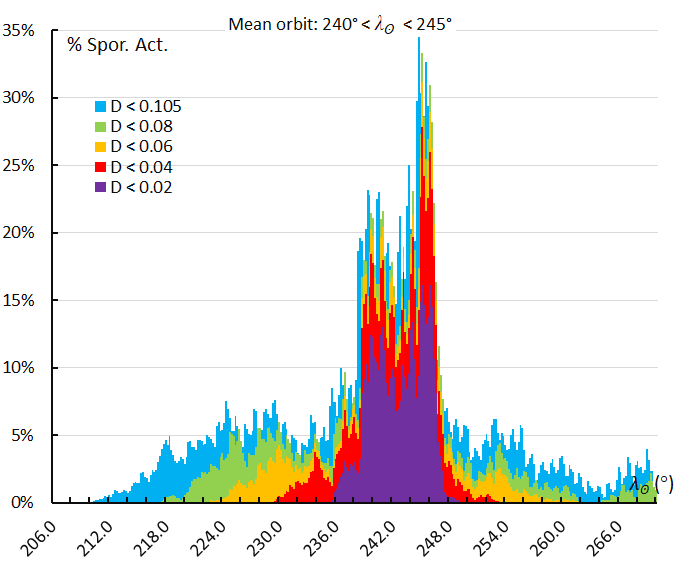
Figure 70 – The activity profile based on the orbit similarity shower identification using a reference orbit derived for the activity interval 240° < λʘ < 245°.
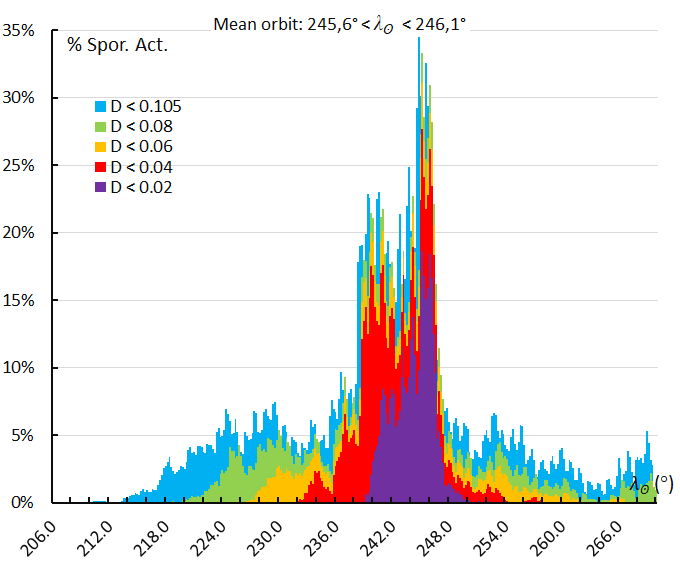
Figure 71 – The activity profile based on the orbit similarity shower identification using a reference orbit derived for the activity interval 245.6° < λʘ < 246.1°, the third and final sharp maximum.
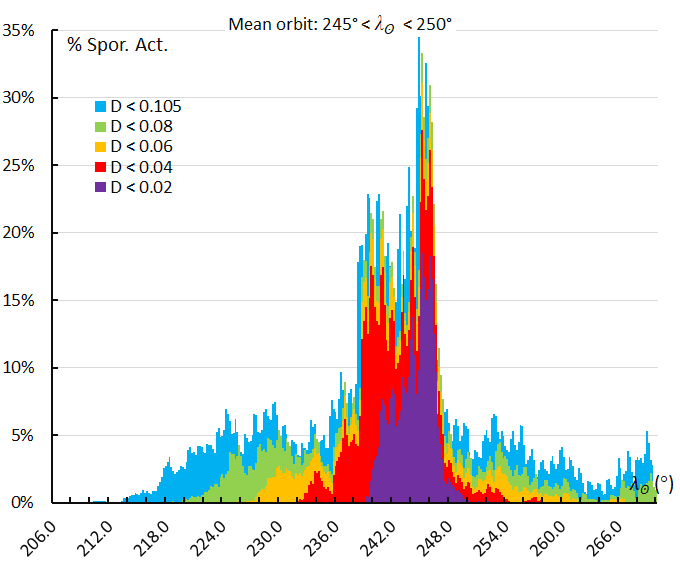
Figure 72 – The activity profile based on the orbit similarity shower identification using a reference orbit derived for the activity interval 245° < λʘ < 250°.
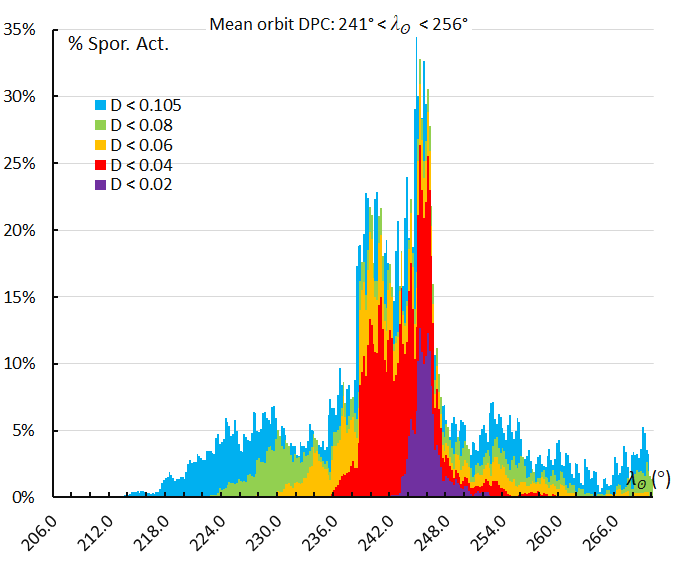
Figure 73 – The activity profile based on the orbit similarity shower identification using a reference orbit derived for the activity interval 241° < λʘ < 256° with the December psi Cassiopeiid orbits identified by GMN.
Conclusions
The analysis of the available Andromedid and December psi Cassiopeiid orbits obtained by the Global Meteor Network allowed a detailed picture to be established of the structure of this stream during the enhanced activity observed during 2021. The hourly rates remained very low at 35% of the sporadic rates at best. This is barely noticeable for an uninformed visual observer.
The activity period could be confirmed for at least the interval 206° < λʘ < 278° or roughly October 20 till end of December. This activity period is considerably longer than previously assumed and definitely longer than what has been assumed for the automatic GMN shower identification. The shower meteors were identified according to the GMN shower association and independently with the orbit similarity method. Although the latter identifies almost twice as many Andromedid orbits than the GMN method, all essential conclusions in this study remain the same for both identification methods.
The activity profile reveals three different maxima, a first enhanced activity during several nights around λʘ ~234°, a second more compact concentration at λʘ ~239.4° and a final short duration concentration at λʘ ~246.0°. Beyond these time intervals, the activity remained very low at less than 5% of the sporadic activity.
The usual radiant drift caused by the rotation of the Earth around the Sun is partly compensated by the changing orbital orientation. This explains the disagreement in radiant drift between different sources as these depend on the activity interval taken into consideration for the radiant drift. In case of the Andromedids, the radiant drift cannot be determined with an ordinary linear regression with a steady increment in R.A. and declination.
The orbital elements show an evolution in time, the longitude of perihelion Π, the inclination i, and especially the perihelion distance q increase during the activity period. The eccentricity e decreases and the semi major axis a remains constant. The distribution of the orbital elements shows distinct concentrations within the Andromedid complex.
A single reference orbit and radiant position cannot identify all shower members. A range of orbits or an orbit matrix is required to cover the structure of this complex shower. The influence of the choice of the reference orbit on the identification of Andromedid orbits has been shown. Taking the drift in orbital elements into account to define a set of reference orbits to apply the D-criteria could result in an improved shower identification. It is not expected that this would lead to significant different conclusions. It is obvious that the Andromedid meteoroid stream suffered severe perturbations to an extent that it should be considered as a shower complex rather than as a single meteoroid stream.
Acknowledgment
This report is based on the data of the Global Meteor Network which is released under the CC BY 4.0 license. The GMN project is volunteers’ work. All hardware is purchased and all operational costs are covered by the participants themselves. The authors thank the camera operators and everyone who has been somehow contributing to the Global Meteor Network for their efforts to keep the network operational: Richard Abraham, Victor Acciari, Rob Agar, David Akerman, Daknam Al-Ahmadi, Jamie Allen, Alexandre Alves, Željko Andreić, Martyn Andrews, Miguel Angel Diaz, Enrique Arce, Georges Attard, Chris Baddiley, David Bailey, Roger Banks, Hamish Barker, Jean-Philippe Barrilliot, Richard Bassom, Ricky Bassom, Ehud Behar, Josip Belas, Alex Bell, Serge Bergeron, Denis Bergeron, Jorge Bermúdez Augusto Acosta, Steve Berry, Adrian Bigland, Chris Blake, Arie Blumenzweig, Ventsislav Bodakov, Claude Boivin, Robin Boivin, Bruno Bonicontro, Fabricio Borges, Ubiratan Borges, Dorian Božičević, David Brash, Ed Breuer, Martin Breukers, John W. Briggs, Peter G. Brown, Laurent Brunetto, Tim Burgess, Ludger Börgerding, Sylvain Cadieux, Peter Campbell-Burns, Andrew Campbell-Laing, Pablo Canedo, Seppe Canonaco, Jose Carballada, Steve Carter, David Castledine, Gilton Cavallini, Brian Chapman, Jason Charles, Matt Cheselka, Tim Claydon, Trevor Clifton, Manel Colldecarrera, Michael Cook, Bill Cooke, Christopher Coomber, Brendan Cooney, Edward Cooper, Jamie Cooper, Andrew Cooper, Marc Corretgé Gilart, Paul Cox, Llewellyn Cupido, Christopher Curtis, Ivica Ćiković, Dino Čaljkušić, Chris Dakin, Alfredo Dal’Ava Júnior, James Davenport, Richard Davis, Steve Dearden, Christophe Demeautis, Bart Dessoy, Paul Dickinson, Ivo Dijan, Pieter Dijkema, Tammo Jan Dijkema, Marcelo Domingues, Stacey Downton, Zoran Dragić, Iain Drea, Igor Duchaj, Jean-Paul Dumoulin, Garry Dymond, Jürgen Dörr, Robin Earl, Howard Edin, Ollie Eisman, Carl Elkins, Peter Eschman, Bob Evans, Andres Fernandez, Barry Findley, Rick Fischer, Richard Fleet, Jim Fordice, Jean Francois Larouche, Kyle Francis, Patrick Franks, Gustav Frisholm, Enrique Garcilazo Chávez, José García María, Mark Gatehouse, Ivan Gašparić, Chris George, Megan Gialluca, Kevin Gibbs-Wragge, Jason Gill, Philip Gladstone, Uwe Glässner, Hugo González, Nikola Gotovac, Neil Graham, Pete Graham, Colin Graham, Sam Green, Bob Greschke, Daniel J. Grinkevich, Larry Groom, Dominique Guiot, Tioga Gulon, Margareta Gumilar, Peter Gural, Nikolay Gusev, Kees Habraken, Alex Haislip, John Hale, Peter Hallett, Graeme Hanigan, Erwin Harkink, Ed Harman, Marián Harnádek, Ryan Harper, David Hatton, Tim Havens, Mark Haworth, Paul Haworth, Richard Hayler, Sam Hemmelgarn, Rick Hewett, Don Hladiuk, Alex Hodge, Simon Holbeche, Jeff Holmes, Nick Howarth, Matthew Howarth, Jeff Huddle, Bob Hufnagel, Roslina Hussain, Russell Jackson, Jean-Marie Jacquart, Jost Jahn, Phil James, Ron James Jr, Nick James, Rick James, Ilya Jankowsky, Alex Jeffery, Klaas Jobse, Richard Johnston, Dave Jones, Fernando Jordan, Vladimir Jovanović, Jocimar Justino de Souza, Javor Kac, Richard Kacerek, Milan Kalina, Jonathon Kambulow, Steve Kaufman, Paul Kavanagh, Alex Kichev, Harri Kiiskinen, Jean-Baptiste Kikwaya, Sebastian Klier, Dan Klinglesmith, John Kmetz, Zoran Knez, Korado Korlević, Stanislav Korotkiy, Danko Kočiš, Josip Krpan, Zbigniew Krzeminski, Patrik Kukić, Reinhard Kühn, Remi Lacasse, Gaétan Laflamme, Steve Lamb, Hervé Lamy, Jean Larouche Francois, Ian Lauwerys, David Leurquin, Gareth Lloyd, Rob Long De Corday, Eric Lopez, Jose Lopez Galindo, José Luis Martin, Juan Luis Muñoz, Pete Lynch, Frank Lyter, Anton Macan, Jonathan Mackey, John Maclean, Igor Macuka, Nawaz Mahomed, Simon Maidment, Mirjana Malarić, Nedeljko Mandić, Alain Marin, Bob Marshall, Colin Marshall, Andrei Marukhno, Keith Maslin, Nicola Masseroni, Bob Massey, Jacques Masson, Damir Matković, Filip Matković, Dougal Matthews, Michael Mazur, Sergio Mazzi, Stuart McAndrew, Alex McConahay, Robert McCoy, Charlie McCormack, Mark McIntyre, Peter Meadows, Edgar Merizio Mendes, Aleksandar Merlak, Filip Mezak, Pierre-Michael Micaletti, Greg Michael, Matej Mihelčić, Simon Minnican, Wullie Mitchell, Edson Morales Valencia, Nick Moskovitz, Dave Mowbray, Andrew Moyle, Gene Mroz, Muhammad Muharam Luqmanul Hakim, Brian Murphy, Carl Mustoe, Przemek Nagański, Jean-Louis Naudin, Damjan Nemarnik, Attila Nemes, Dave Newbury, Colin Nichols, Nick Norman, Philip Norton, Zoran Novak, Gareth Oakey, Washington Oliveira, Angélica Olmos López, Jamie Olver, Christine Ord, Nigel Owen, Michael O’Connell, Dylan O’Donnell, Thiago Paes, Carl Panter, Neil Papworth, Filip Parag, Gary Parker, Simon Parsons, Ian Pass, Igor Pavletić, Lovro Pavletić, Richard Payne, Pierre-Yves Pechart, William Perkin, Enrico Pettarin, Alan Pevec, Mark Phillips, Patrick Poitevin, Tim Polfliet, Derek Poulton, Janusz Powazki, Aled Powell, Alex Pratt, Miguel Preciado, Chuck Pullen, Terry Pundiak, Lev Pustil’Nik, Dan Pye, Chris Ramsay, David Rankin, Steve Rau, Dustin Rego, Chris Reichelt, Danijel Reponj, Fernando Requena, Maciej Reszelsk, Ewan Richardson, Martin Richmond-Hardy, Mark Robbins, David Robinson, Martin Robinson, Heriton Rocha, Herve Roche, Adriana Roggemans, Paul Roggemans, Alex Roig, David Rollinson, Jim Rowe, Dmitrii Rychkov, Michel Saint-Laurent, Clive Sanders, Jason Sanders, Ivan Sardelić, Rob Saunders, John Savage, Lawrence Saville, Vasilii Savtchenko, William Schauff, Ansgar Schmidt, Jim Seargeant, Jay Shaffer, Steven Shanks, Mike Shaw, Angel Sierra, Ivo Silvestri, Ivica Skokić, Dave Smith, Tracey Snelus, Warley Souza, Mark Spink, Denis St-Gelais, James Stanley, Radim Stano, Laurie Stanton, Rob Steele, Yuri Stepanychev, Graham Stevens, Peter Stewart, William Stewart, Con Stoitsis, Andrea Storani, Andy Stott, David Strawford, Rajko Sušanj, Bela Szomi Kralj, Marko Šegon, Damir Šegon, Jeremy Taylor, Yakov Tchenak, Eric Toops, Torcuill Torrance, Steve Trone, Wenceslao Trujillo, John Tuckett, Myron Valenta, Jean Vallieres, Paraksh Vankawala, Neville Vann, Marco Verstraaten, Arie Verveer, Denis Vida, Predrag Vukovic, Martin Walker, Aden Walker, Bill Wallace, John Waller, Jacques Walliang, Didier Walliang, Jacques Walliang, Christian Wanlin, Tom Warner, Neil Waters, Steve Welch, Alexander Wiedekind-Klein, John Wildridge, Ian Williams, Guy Williamson, Urs Wirthmueller, Bill Witte, Martin Woodward, Jonathan Wyatt, Anton Yanishevskiy, Penko Yordanov, Stephane Zanoni, Dario Zubović, Pierre de Ponthière, Erwin van Ballegoij, Edison Álvarez José Felipe Pérezgómez.
References
Drummond J. D. (1981). “A test of comet and meteor shower associations”. Icarus, 45, 545–553.
Jenniskens P. (2006). Meteor Showers and their Parent Comets. Cambridge, UK: Cambridge University Press, 2006.
Jenniskens P., Vaubaillon J. (2007). “3D/Biela and the Andromedids: Fragmenting versus Sublimating Comets”. Astronomical Journal, 134, 1037–1045.
Jenniskens P., Nénon Q., Albers J., Gural P. S., Haberman B., Morales R., Grigsby B. J., Samuels D., Johannink C. (2016). “The established meteor showers as observed by CAMS”. Icarus, 266,
331–354.
Jenniskens P., Baggaley J., Crumpton I., Aldous P., Pokorny P., Janches D., Gural P. S., Samuels D., Albers J., Howell A., Johannink C., Breukers M., Odeh M., Moskovitz N., Collison J. and Ganjuag S. (2018). “A survey of southern hemisphere meteor showers”. Planetary Space Science, 154, 21–29.
Jenniskens P. (2022a). “An outburst of Andromedids (AND#0018) in 2021”. eMetN, 7, 1–2.
Jenniskens P. and Moskovitz N. (2022b). “An outburst of Andromedids on November 28, 2021”. eMetN, 7,
3–5.
Jopek T. J. (1993). “Remarks on the meteor orbital similarity D-criterion”. Icarus, 106, 603–607.
Jopek T. J., Rudawska R. and Pretka-Ziomek H. (2006). “Calculation of the mean orbit of a meteoroid stream”. Monthly Notices of the Royal Astronomical Society, 371, 1367–1372.
Koseki M. (2021). “The activity of meteor showers recorded by SonotaCo Net video observations 2007–2018, AND (#0018)”. eMetN, 6, 185–186.
Kronk G. (1988). “Meteor Showers: A Descriptive Catalog”. Hillside, New Jersey, USA: Enslow Publishers.
Moorhead A., Clements T.D. and Vida D. (2020). “Realistic gravitational focusing of meteoroid streams”. Monthly Notices of the Royal Astronomical Society, 494, 2982–2994.
Roggemans P., Johannink C. and Cambell-Burns P. (2019). “October Ursae Majorids (OCU#333)”. eMetN, 4, 55–64.
SonotaCo (2009). “A meteor shower catalog based on video observations in 2007-2008”. WGN, Journal of the International Meteor Organization, 37, 55–62
Southworth R. R. and Hawkins G. S. (1963). “Statistics of meteor streams”. Smithson. Contrib. Astrophys., 7, 261–286.
Vida D., Šegon D., Gural P. S., Brown P. G., McIntyre M. J. M., Dijkema T. J., Pavletić L., Kukić P., Mazur M. J., Eschman P., Roggemans P., Merlak A., Zubrović D. (2021). (2021). “The Global Meteor Network – Methodology and first results”. Monthly Notices of the Royal Astronomical Society, 506 (4),
5046–5074.
Wiegert P. A., Brown P. G., Weryk R. J., Wong D. K. (2013). “The return of the Andromedids meteor shower”. Astronomical Journal, 145, 70–81.