Ventsislav Bodakov
Stellar Society, Bulgaria
Abstract: At 23h58m UTC on 2024, November 19 a bright fireball was observed over Bulgaria by three Global Meteor Network cameras. The trajectory and orbit were computed. The orbit is inclined by 54 degrees and is extending beyond Saturn.
INTRODUCTION
Long time has passed since the last fireball was registered by the Bulgarian GMN cameras. That is why, when I was routinely checking the GMN camera status page and noticed the bright event I knew it might be interesting to analyze. One camera (BG000D) recorded the entire track of the fireball (Figure 1), another one (BG0004) up to the moment of the explosion (Figure 2), and a third one (BG0003) – part of it through the clouds (Figure 3).

Figure 1 – The fireball as seen from BG000D.

Figure 2 – The fireball as seen from BG0004.
Although the first two cameras captured the event, the brightness of the fireball saturating the camera sensor and the explosion itself made the meteor detector algorithm to not regard this as a regular meteor. The algorithm seeks the frames for a well-defined “centroid” of a meteor, which is hard or impossible to be determined in case of an overexposed, exploding fireball. Consequently, there was no detection entry in *radiants.txt, no presence in the detected stack and no FF file in Archive directory. However, the brightness of the event triggered the fireball detector and it created an uncompressed “region-of-interest” video as FR file in the Archive directory. The third camera (BG0003) observed the meteor through cloud which greatly reduced the brightness and the meteor detection algorithm registered it. This effect helped for the accuracy of the trajectory estimation as we will see below.

Figure 3 – The fireball as seen from BG0003.
FIREBALL ANALYSIS
In such cases when a fireball is not detected by the algorithm at the meteor station and a detailed report and orbit estimation is needed, a manual reduction of the meteor data should be done. The data produced should then be correlated with a trajectory solver – in this case – Western Meteor Python Library. WMPL is a data analysis suite with the purpose of trajectory solving and orbit estimation, developed by the Western Meteor Physics Group at the University of Western Ontario.
The manual reduction of the fireball was done using SkyFit2, part of the RMS software of GMN meteor stations. The software was installed on Ubuntu 20.04.6 LTS virtual machine, along with the WMPL trajectory solver. The data reduction for BG000D and BG0004 was done using the FR files produced by the fireball detector in each station, which being uncompressed are better for the purpose compared to the compressed FF files. For a better accuracy first the field of view was recalibrated using the visible stars. Then the position of the fireball’s centroid was marked in each frame. Once this process is done for each camera, SkyFit2 generates respective ECSV files as a result. This file contains data about the meteor position as coordinates in time. As a second step in multi-station analysis these ECSV files were then analyzed and solved by WMPL with the additional option of 20 runs of the Monte Carlo method for a possible optimization of the error margins (Vida et al., 2019; 2020; 2021).
RESULTS
The computed convergence angles between the planes of each camera and the fireball are all above the minimum of 3 degrees for a successful trajectory estimation. For BG0004 and BG000D it is 9.8 degrees, BG0003 and BG0004 – 15 degrees, and for BG0003 and BG000D – 25 degrees, which makes it the best intersection. A Google Earth 3D visualization of the trajectory and the plane intersections was generated with WMPL’s Utils.TrajectoryKML tool (Figure 4).
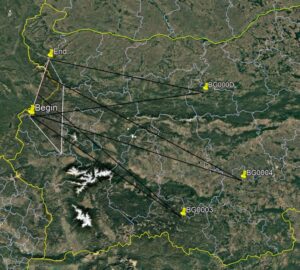
Figure 4 – Google Earth 3D visualization of the fireball trajectory.
The spatial residuals for BG000D, BG0004 and BG0003 are shown in Figures 5, 6 and 7, respectively. What attracts attention is that BG0003 has an excellent horizontal RMS deviation of 0.73m, possibly due to the well-defined fireball track dimmed by the clouds, allowing for a precise manual data reduction.
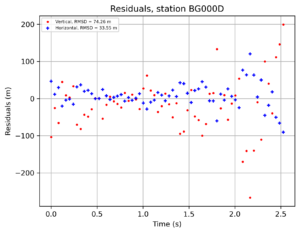
Figure 5 – BG000D spatial residuals.
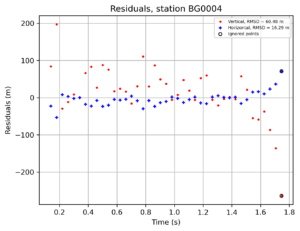
Figure 6 – BG0004 spatial residuals.
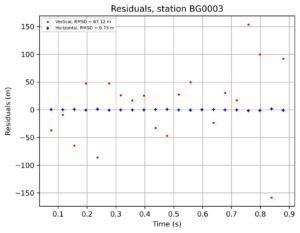
Figure 7 – BG0003 spatial residuals.
The meteoroid entered the atmosphere at an angle of 31.2 degrees, with an initial velocity of 40.3 km/s, burning up at an altitude between 114.9 km and 63.9 km. The detailed begin and end points of the trajectory with 95% confidence intervals are listed in Table 1.
Table 1 – End points of the fireball trajectory.
| Parameters | Position |
| Latitude begin (°) | 42.382274 ± 0.0001 (± 14.02 m) |
| Longitude begin (°) | 23.102409 ± 0.0005 (± 38.95 m) |
| Height begin (m) | 114918.85 ± 45.70 |
| Latitude end (°) | 43.148521 ± 0.0001 (± 16.44 m) |
| Longitude end (°) | 23.070114 ± 0.0008 (± 66.76 m) |
| Height end (m) | 63940.58 ± 44.83 |
Figure 8 shows a ground track representation of the fireball and the cameras that observed it. The black cross marks the lowest height at which the fireball was captured.
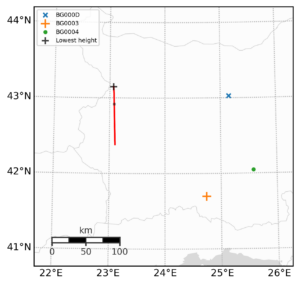
Figure 8 – Ground track of the fireball.
The orbit estimation shows that the fireball had an orbit extending beyond Saturn with an inclination of 54 degrees relative to the ecliptic – Figures 9 and 10.
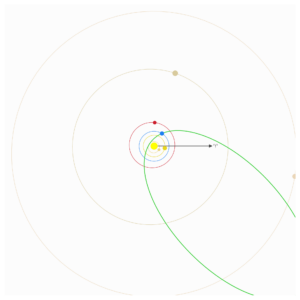
Figure 9 – The fireball orbit, top view.

Figure 10 – The fireball orbit, side view.
No meteor shower could be associated therefore this fireball has been classified as a sporadic. The detailed orbital elements with 95% confidence intervals are specified in Table 2.
Table 2 – Orbital elements of the fireball.
| Parameter | Value |
| Epoch JD | 2460634.499 |
| Solar longitude (λ☉) | 237.809° |
| R.A. (αg) | 83.10 ± 0.05° |
| Dec. (δg) | –17.97 ± 0.04° |
| Geocentric velocity (vg) | 38.783 ± 0.015 km/s |
| λg | 81.26 ± 0.06° |
| βg | –41.20 ± 0.04 |
| λg – λʘ | 203.45 ± 0.06° |
| Semi-major axis (a) | 13.7 ± 0.4 AU |
| Perihelion distance (q) | 0.55917 ± 0.0005 AU |
| Eccentricity (e) | 0.959 ± 0.001 |
| Inclination (i) | 54.058 ± 0.037° |
| Longitude of ascending node (Ω) | 57.811 ± 0.000002° |
| Argument of perihelion (ω) | 83.491 ± 0.049° |
| Longitude of perihelion (Π) | 141.30 ± 0.05° |
| Mean anomaly (M) | 359.245 ± 0.036° |
| Orbital period (T) | 50.57 ± 2.28 years |
| Tisserand’s parameter (Tj) | 0.919 ± 0.011 |
DISCUSSION
The calculated Tisserand’s parameter with respect to Jupiter as perturbing body indicates a cometary Mellish-type object with Tj = 0.919.
The estimated orbit aphelion beyond Saturn may suggest that the object could be a “centaur” perturbed into this orbit by the giant planets. However, this cannot be proven with the current observation data.
ACKNOWLEDGMENTS
I would like to thank Yozhi Nasvadi and Penko Yordanov for providing the data from their RMS cameras and Paul Roggemans for his valuable help for writing this report.
REFERENCES
Vida D., Gural P., Brown P., Campbell-Brown M., Wiegert P. (2019). “Estimating trajectories of meteors: an observational Monte Carlo approach – I. Theory”. Monthly Notices of the Royal Astronomical Society, 491, 2688–2705.
Vida D., Gural P., Brown P., Campbell-Brown M., Wiegert P. (2020). “Estimating trajectories of meteors: an observational Monte Carlo approach – II. Results”. Monthly Notices of the Royal Astronomical Society, 491, 3996–4011.
Vida D., Šegon D., Gural P. S., Brown P. G., McIntyre M. J. M., Dijkema T. J., Pavletić L., Kukić P., Mazur M. J., Eschman P., Roggemans P., Merlak A., Zubrović D. (2021). “The Global Meteor Network – Methodology and first results”. Monthly Notices of the Royal Astronomical Society, 506, 5046–5074.

