By Damir Šegon, Denis Vida and Paul Roggemans
Abstract: A new meteor shower on a Jupiter-family comet orbit (TJ = 2.9 ± 0.1) orbit has been detected during October 26–27, 2024 by the Global Meteor Network. Meteors belonging to the new shower were observed between 213.4° < λʘ < 214° from a radiant at R.A. = 289° and Decl.= +37° in the constellation of Lyra, with a geocentric velocity of 13 km/s. The new meteor shower has been listed in the Working List of Meteor Showers under the temporary name-designation: M2024-U1.
Introduction
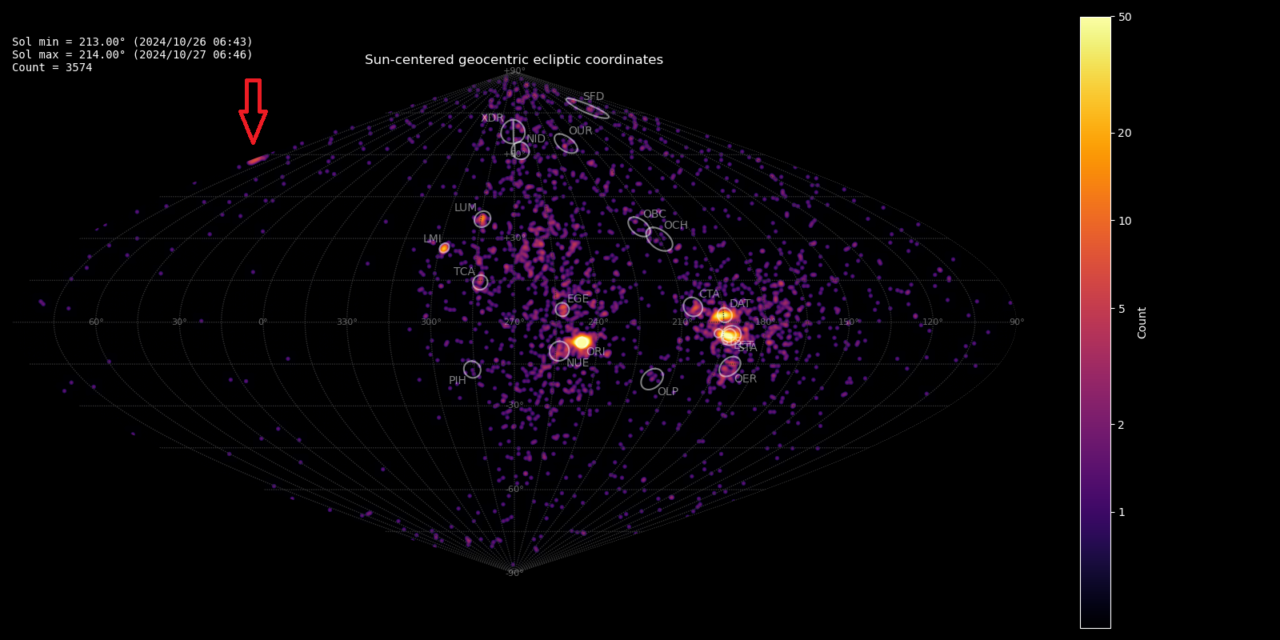
An unexpected concentration of radiants appeared on the radiant plot of the Global Meteor Network data for 2024 October 26–27 in Sun-centered geocentric ecliptic coordinates. No trace of this activity could be seen on these maps for previous or later days. A first analysis identified 17 meteors within a narrow time interval of about a half day, between solar-longitude interval 213.42° – 213.94°, with a peak around 213.55°. The shower was independently observed by cameras in 9 countries across the globe (Belgium, Canada, France, Germany, Greece, Romania, the Netherlands, United Kingdom and the USA). A CBET announcement was prepared and published (Vida and Šegon, 2024) and the new meteor shower was registered by the IAU Meteor Data Center and got the temporary identification M2024-U1.
Figure 1 – Radiant plot of the Global Meteor Network data for 2024 October 26–27 in Sun-centered geocentric ecliptic coordinates. The new radiant is visible at the edge of the map and marked by a red arrow.
Discovery and first analysis
We used the procedure as described for some recent cases of possibly new showers in Bootes and Draco (Šegon et al., 2023). The Drummond dissimilarity criteria DD has been chosen for the analysis of the new radiant concentration. A first iteration revealed a clear concentration of orbits, as it can be seen on Figure 2. The Rayleigh distribution fit pointed at a DD value of 0.01 as the orbital similarity cutoff (Figure 3), which is unusually narrow and resulted in 17 orbits representing the possibly new meteor shower.
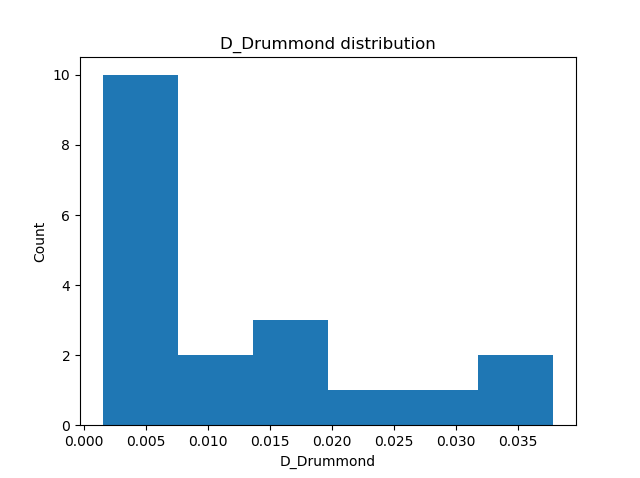
Figure 2 – Histogram of the distribution of the Drummond DD criterion values valid for the final mean orbit.
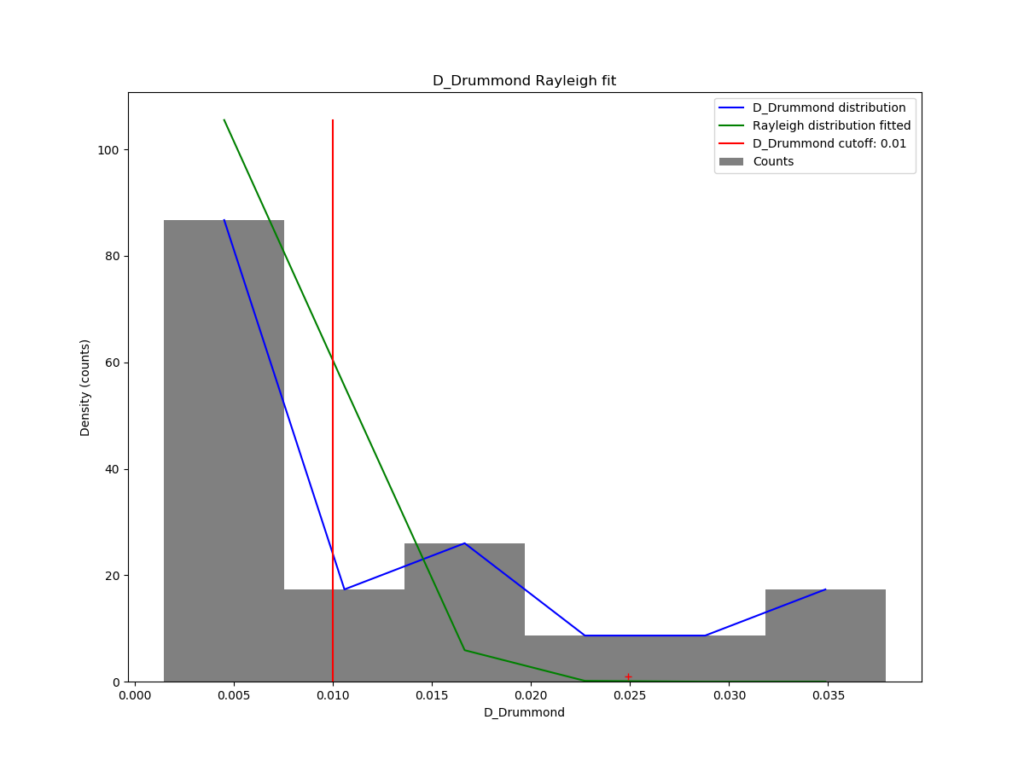
Figure 3 – Rayleigh distribution fit and Drummond DD criterion cutoff with an exceptional narrow discriminiation interval.
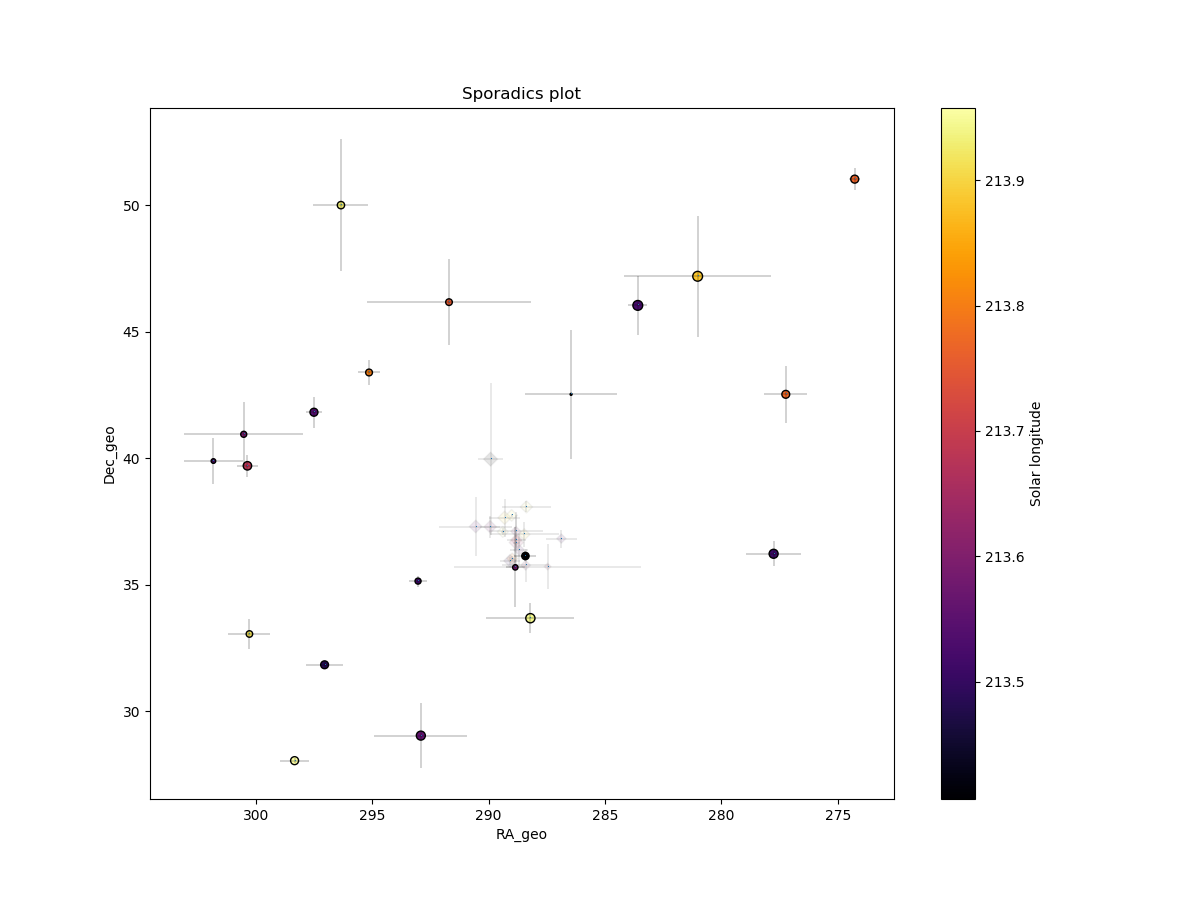
Figure 4 – All non shower meteor radiants in geocentric equatorial coordinates during the shower activity. The pale diamonds represent the new shower radiants plots, error bars represent two sigma values in both coordinates.
The presence of non-shower radiants in the area around the possibly new shower (Figure 4) shows the cutoff to be reliable since the density of meteor radiants does not look affected after removing shower members (plotted as pale diamonds). The plot of the shower meteor radiants in equatorial coordinates shows a very compact group (see Figure 5). The Π–i diagram also shows a compact group of radiants (Figure 6), without any other groups of radiants to be seen.
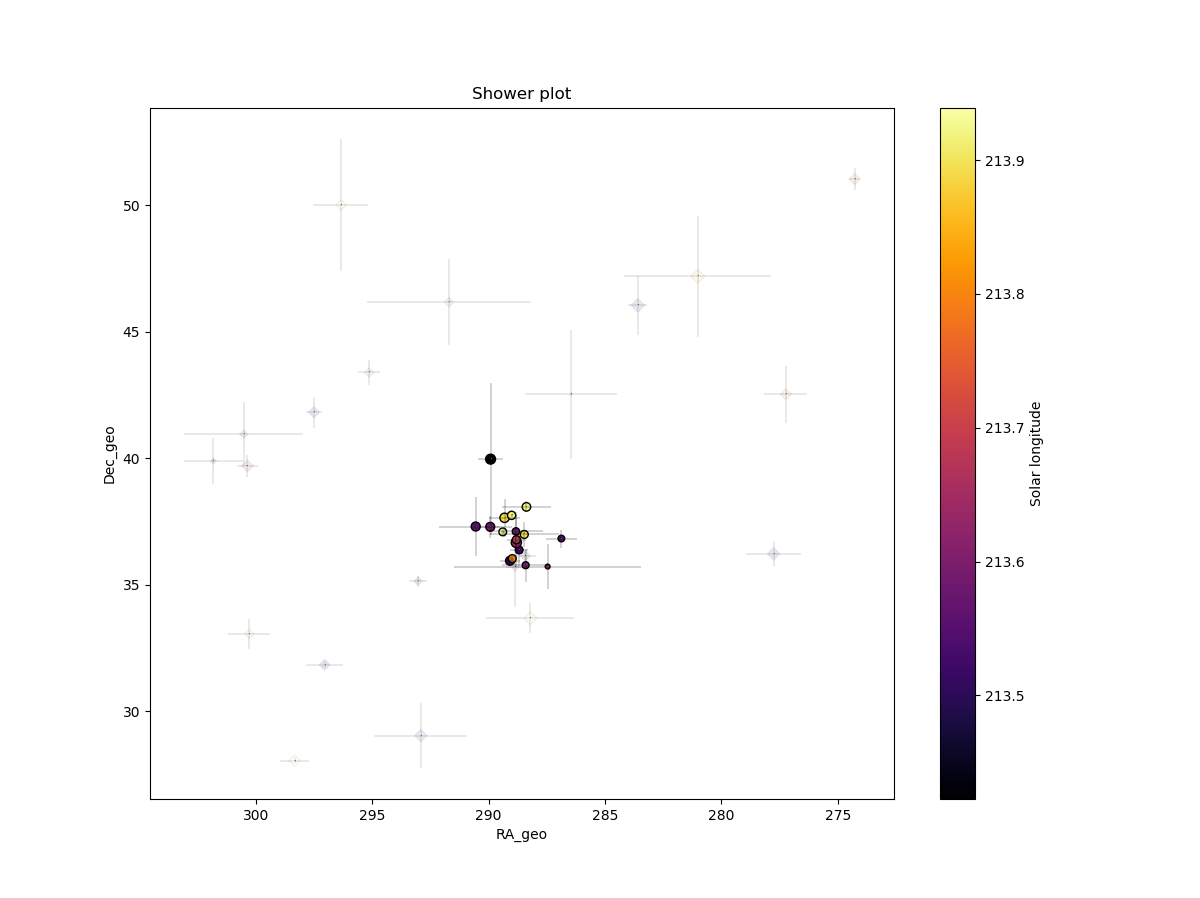
Figure 5 – The reverse of Figure 4, now the shower meteors are shown as circles and the non shower meteors as grayed out diamonds. Note that there are no other groups of meteor radiants to be seen in the vicinity of the possibly new meteor shower.
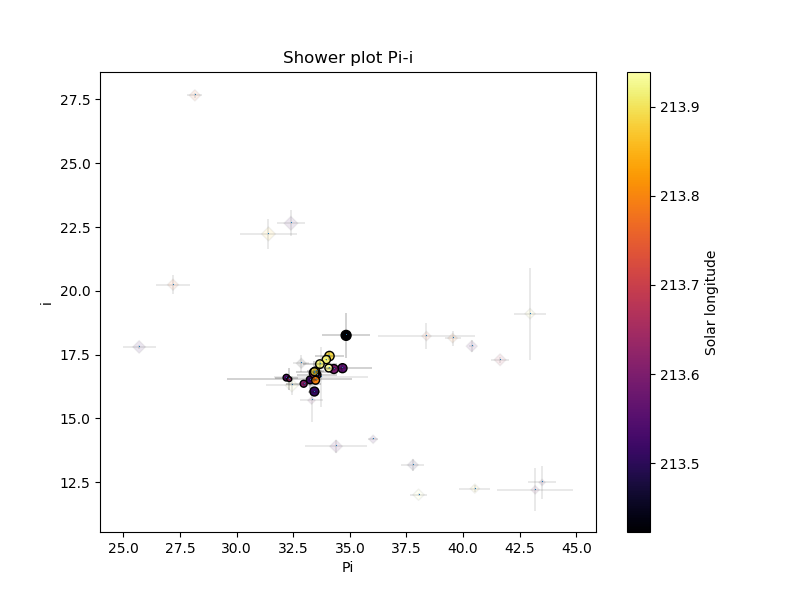
Figure 6 – The diagram of the inclination i against longitude of perihelion Π shows a distinct group of radiants without any other groups to be seen.
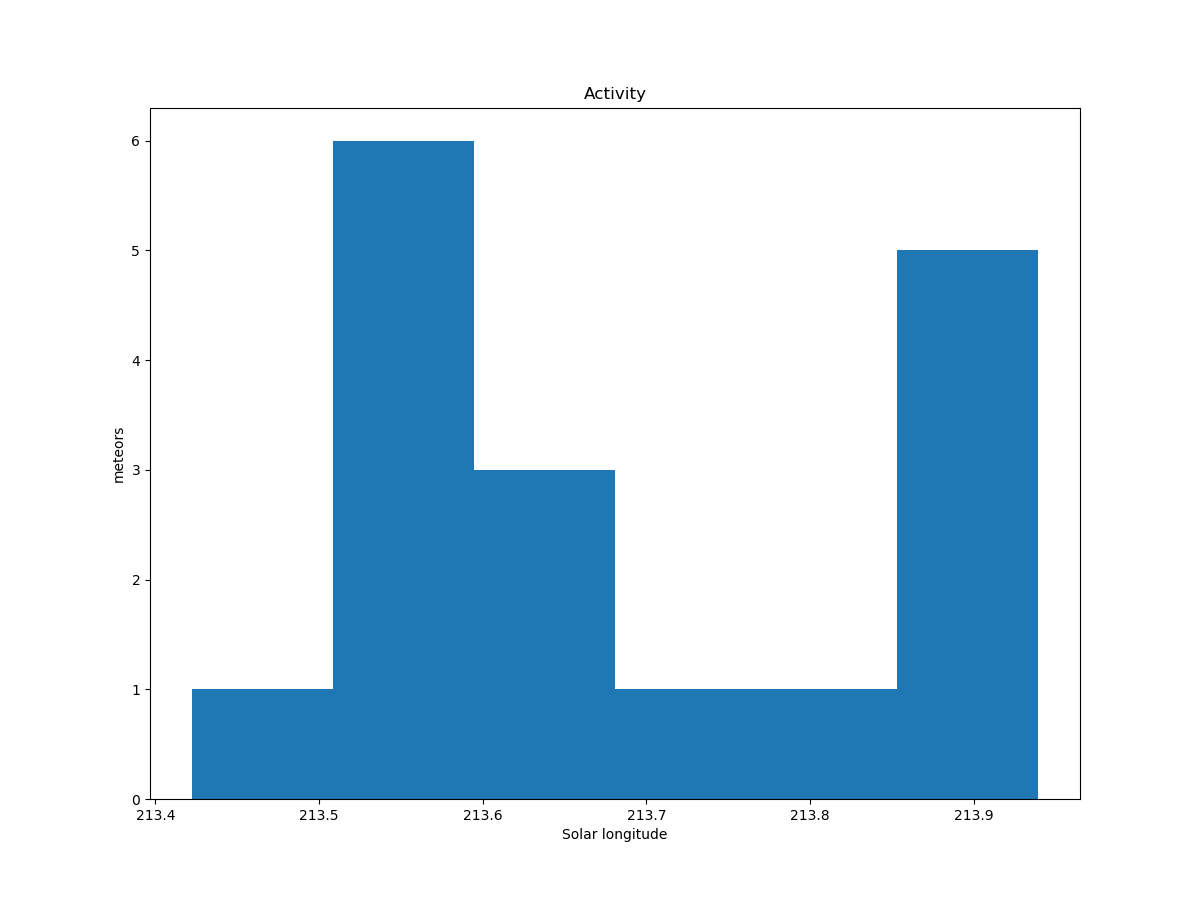
Figure 7 – The activity period with the number of orbits identified as new shower members.
The activity period (Figure 7) was limited to the interval 213.4° < λʘ < 214° (2024, October 26–27). The first analysis provided solid proof that a thus far unknown shower had been detected.
Looking for similar orbits of known meteor showers in the IAU MDC list of meteor showers, the best matching case with DD = 0.05 are the delta-Cygnids (DCY#0282). However, this meteor shower had been removed from the working list because no original references were given for it. Moreover, the orbit was based on as few as 5 orbits which is far too little to define a meteor shower. Its activity date at λʘ = 200.8° differs about two weeks from the detected new meteor shower and the radiant positions are far apart. A second matching meteor shower with DD = 0.06, the October Cygnids (OCG#0083) is even further off in both activity period and radiant position. The third possible match with DD = 0.07 for the iota-Cygnids (ICY#0525) is closer in time with λʘ = 218.4°, but the radiant position differs too much. Andreic et al. (2013) concluded that the radiant plot was very diffuse and that all three above mentioned meteor showers are most probably just one shower. It should be noted that the available discrimination criteria are very tricky with this type of low inclination Jupiter Family Comet orbits. There are plenty of this type of orbits that may produce pure chance D-criteria matches. We can conclude that no known meteor shower can be associated with the newly detected activity.
Table 1 – The new meteor shower, derived by two different methods.
| New (Šegon) | New (Roggemans) | ||
| DD < 0.02 | DD < 0.01 | ||
| λʘ (°) | 213.55 | 213.64 | 213.63 |
| λʘb (°) | 213.42 | 210.6 | 210.6 |
| λʘe (°) | 213.94 | 222.4 | 213.94 |
| αg (°) | 288.9 | 289.0 | 289.0 |
| δg (°) | +37.0 | +37.1 | +37.0 |
| Δαg (°) | – | – | – |
| Δδg (°) | – | – | – |
| vg (km/s) | 13.1 | 13.1 | 13.1 |
| λ (°) | 299.7 | 300.2 | 299.8 |
| λg – λʘ (°) | 86.0 | 86.3 | 86.0 |
| βg (°) | +58.2 | +58.5 | +58.5 |
| a (A.U.) | 2.88 | 2.91 | 2.91 |
| q (A.U.) | 0.9938 | 0.9932 | 0.9938 |
| e | 0.6545 | 0.6598 | 0.6589 |
| i (°) | 16.9 | 16.8 | 17.0 |
| ω (°) | 179.9 | 180.3 | 180.5 |
| Ω (°) | 213.7 | 213.9 | 213.3 |
| Π (°) | 33.6 | 34.2 | 33.8 |
| Tj | 2.89 | 2.86 | 2.86 |
| N | 17 | 23 | 14 |
Another search method
Another method has been applied to check this new meteor shower discovery. The starting point here can be any visually spotted concentration of radiant points or any other indication for the occurrence of similar orbits. The method has been described before (Roggemans et al., 2019). The main difference with the method applied in Section 2 is that three different discrimination criteria are combined in order to have only those orbits which fit different criteria. The D-criteria that we use are these of Southworth and Hawkins DSH (1963), Drummond DD (1981) and Jopek DJ (1993) combined. Instead of using a cutoff value for the D-criteria these values are considered in different classes with different thresholds of similarity. Depending on the dispersion and the type of orbits, the most appropriate threshold of similarity is selected to locate the best fitting mean orbit as the result of an iterative procedure.
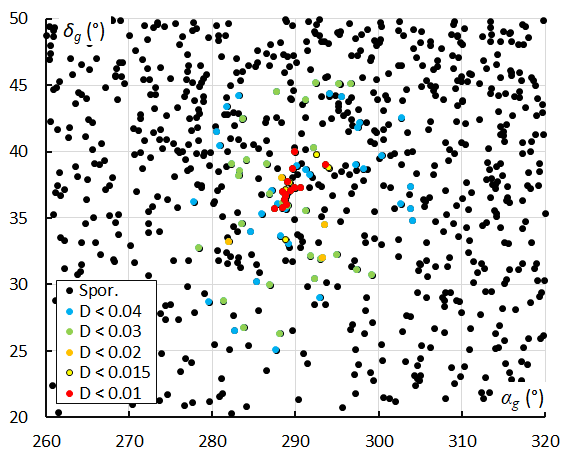
Figure 8 – Radiant plot in geocentric equatorial coordinates for different similarity thresholds, This plot shows all radiant points collected in solar longitude between 196°–228°.
This method detects 84 candidate orbits with similarity criteria better than DD < 0.04, DSH < 0.1 and DJ < 0.1, detected during a time interval of about a month, 196° < λʘ < 228°. Figure 8 shows all the radiants detected during this interval, the spread in time and dispersion of the radiant points suggests that most of these orbits marked in blue (DD < 0.04) and green (DD < 0.03) are sporadics that fit the D-criteria by pure chance. The explanation for this is in the type of orbits, low inclination JFC orbits. The usual cutoff values for D-criteria orbit similarities are not valid for this type of orbits. With other words, using D-criteria in this case is tricky and requires a careful approach to avoid combining randomly unassociated orbits into a new shower detection. This may explain the unconfirmed origin of the neighboring meteor showers found in the IAU MDC working list of meteor showers based on poorly interpreted D-criteria.
The DSH and DJ criteria are not very helpful for these types of orbits. For this case we must consider more strict similarity classes with the Drummond DD criterion as main discriminator. We consider the following classes:
- DD< 0.03, DSH < 0.05 and DJ < 0.05 (green dots);
- DD< 0.02, DSH < 0.05 and DJ < 0.05 (orange dots);
- DD< 0.015, DSH < 0.05 and DJ < 0.05 (yellow dots);
- DD< 0.01, DSH < 0.05 and DJ < 0.05 (red dots).
In Figure 8 we see a concentration of radiants with DD values better than DD < 0.02. This is also very obvious in Figure 9 where we plot the radiants limited to the interval 210° < λʘ < 215°. The concentration is also very well visible in the diagram of the inclination i against the longitude of perihelion Π (Figure 10). 14 of the 19 orbits with DD < 0.015 were detected during the interval, 213.4° < λʘ < 214.0°, four more were detected earlier and one later.
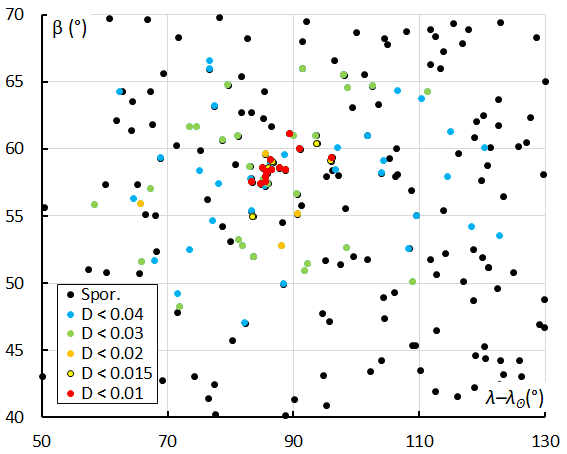
Figure 9 – Radiant plot in geocentric Sun-centered ecliptic coordinates for different similarity thresholds. This plot shows all radiant points collected in solar longitude between 210°–215°.
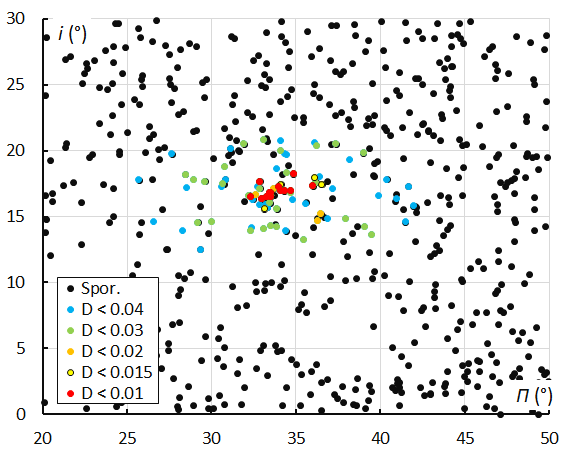
Figure 10 – Diagram of the inclination i against the longitude of perihelion Π. This plot shows all radiant points collected in solar longitude between 210°–215°.
The mean orbit computed according to Jopek et al. (2006) for the orbits selected using the method of Šegon et al. (2023) is listed as New (Šegon) in Table 1, the mean orbit for the selection using the method of Roggemans et al. (2019) is listed under New (Roggemans) and compares the mean orbit obtained for DD < 0.02 with the result for DD < 0.01. The dispersion of radiants with less good similarity are also shown in Figures 8 and 9, but these orbits were not used to compute the mean orbit to avoid contamination with sporadics. The three mean orbits are almost identical, so the few outliers detected before and after the main concentration do not influence the final orbit.
Comparing older data and other datasets
Looking up past years orbit data for Global Meteor Network (2018–2023, 1174206 orbits), we find 10 orbits with DD < 0.02. Two in 2019, one in 2020, one in 2021, two in 2022 and four in 2023, spread in time at different solar longitudes several days apart. The SonotaCo net orbit data (2007–2023, 490283 orbits) has only one orbit with DD < 0.02, recorded in 2022. EDMOND (2001–2023, 508266 orbits), has one orbit with DD < 0.02 in 2016. The CAMS orbit data (2010–2016, 471582 orbits), also has one orbit with DD < 0.02, recorded in 2016.
The few similar orbits found in previous years in different datasets all appeared spread in time. There is no trace of any previous recorded annual activity or outburst. These few isolated cases may be just sporadics that fulfill the similarity criteria by pure chance.
Discussion
This new meteor shower is a good example to demonstrate the risks of using discrimination criteria without considering the cutoff value. Any meteoroid stream search on this type of low inclination JFC orbits will result in many positive matching sporadic orbits, good for defining spurious meteor showers. For the same reason the parent body search did not result in any certain association. 2014 UR36 (DSH = 0.07) or 185P/Petriew (DSH = 0.1) were the only two objects with orbit similarity, but again the Southworth and Hawkins criterion is not working well for this type of orbits and the similarity is far from the cutoff value used for the meteoroid orbits.
Meteor showers like this are a challenge to detect as the number of meteors is very low with a radiant near the antapex where meteoroids enter the atmosphere with very low entrance velocities as the particles must catch up with the Earth from the rear. The same particle concentration encountered head-on would produce much faster and thus brighter and easier to detect meteors.
Conclusion
A possibly new meteor shower in the constellation of Lyra active during 213.4° < λʘ < 214°, has been detected in the Global Meteor Network orbit data for October 26–27, 2024. The resulting orbit is a Jupiter-family comet orbit one. The new meteor shower has been listed in the Working List of Meteor Showers under the temporary identification M2024-U1.
Acknowledgment
This report is based on the data of the Global Meteor Network (Vida et al., 2020a; 2020b; 2021) which is released under the CC BY 4.0 license. We thank all 825 participants in the Global Meteor Network project for their contribution and perseverance. This list of operators whose cameras provided the data used in this work and contributors who made important code contributions are mentioned elsewhere in this issue (Šegon et al., 2025).
References
Andreić Ž., Šegon D., Korlević K., Novoselnik F., Vida D., Skokić I. (2013). “Ten possible new showers from the Croatian Meteor Network and SonotaCo datasets”. WGN, Journal of the International Meteor Organization, 41, 103–107.
Drummond J. D. (1981). “A test of comet and meteor shower associations”. Icarus, 45, 545–553.
Jopek T. J. (1993). “Remarks on the meteor orbital similarity D-criterion”. Icarus, 106, 603–607.
Jopek T. J., Rudawska R. and Pretka-Ziomek H. (2006). “Calculation of the mean orbit of a meteoroid stream”. Monthly Notices of the Royal Astronomical Society, 371, 1367–1372.
Jopek T. J., Jenniskens P. M. (2011). “The Working Group on Meteor Showers Nomenclature: A History, Current Status and a Call for Contributions”. In, W.J. Cooke, D.E. Moser, B.F. Hardin, and D. Janches, editors, Meteoroids: The Smallest Solar System Bodies, Proceedings of the Meteoroids Conference held in Breckenridge, Colorado, USA, May 24-28, 2010. NASA/CP-2011-216469, pages 7–13.
Jopek T. J., Kaňuchová Z. (2014). “Current status of the~IAU MDC Meteor Showers Database”. In, T.J. Jopek, F.J.M. Rietmeijer, J. Watanabe, I.P. Williams, editors, Meteoroids 2013 Proceedings of the Astronomical Conference held at A.M. University, Poznan, Poland, Aug. 26-30, 2013, A.M. University Press, pages 353–364.
Jopek T. J., Kaňuchová Z. (2017). “IAU Meteor Data Center-the shower database: A status report”. Planetary and Space Science, 143, 3–6.
Neslušan L., Poručan V., Svoreň J., Jakubík M. (2020). “On the new design of the IAU MDC portal”. WGN, Journal of the International Meteor Organization, 48, 168–169.
Roggemans P., Johannink C. and Campbell-Burns P. (2019a). “October Ursae Majorids (OCU#333)”. eMetN Meteor Journal, 4, 55–64.
Šegon D., Vida D., Roggemans P. (2023). “New meteor shower in Draco”. eMetN Meteor Journal, 8, 171–176.
Šegon D., Vida D., Roggemans P. (2025). “New meteor shower in Ursa Minor”. eMetN Meteor Journal, 10, this issue.
Southworth R. B. and Hawkins G. S. (1963). “Statistics of meteor streams”. Smithsonian Contributions to Astrophysics, 7, 261–285.
Vida D., Gural P., Brown P., Campbell-Brown M., Wiegert P. (2020a). “Estimating trajectories of meteors: an observational Monte Carlo approach – I. Theory”. Monthly Notices of the Royal Astronomical Society, 491, 2688–2705.
Vida D., Gural P., Brown P., Campbell-Brown M., Wiegert P. (2020b). “Estimating trajectories of meteors: an observational Monte Carlo approach – II. Results”. Monthly Notices of the Royal Astronomical Society, 491, 3996–4011.
Vida D., Šegon D., Gural P. S., Brown P. G., McIntyre M. J. M., Dijkema T. J., Pavletić L., Kukić P., Mazur M. J., Eschman P., Roggemans P., Merlak A., Zubrović D. (2021). “The Global Meteor Network – Methodology and first results”. Monthly Notices of the Royal Astronomical Society, 506, 5046–5074.
Vida D., Segon D. (2024). New meteor shower M2024-U1 in Lyra. CBET 5470. D. W. E. Green (ed.), 1 pp.