by Paul Roggemans, Carl Johannink and Takashi Sekiguchi
A short-lived activity enhancement of the Phi Serpentids (PSR#839) allowed to calculate a reliable reference orbit for the 2020 return of this minor shower. The meteors and orbit identification of the Phi Serpentids caused confusion with the κ Serpentids (KSE#027) meteor stream for which the reference orbits were established before the PSR shower was known. The sudden activity with several orbits registered in a short time lapse from a very compact radiant is very likely related to an unknown long periodic comet. Attention should be paid to the PSR shower in the future as more dust may move ahead of the unknown parent body that may be on its way to return. The similarity between the KSE and PSR orbits suggests that these are both dust components of the same parent body.
1 Introduction
When a small compact cluster of radiants appeared on the daily CAMS report screen (http://cams.seti.org/FDL/), it was obvious that one of the minor showers in this region of the sky had suddenly flared up. Peter Jenniskens identified the minor shower φ Serpentids (PSR#839) with the recorded orbits. This was somehow confusing as most camera operators got the κ Serpentids (KSE#027) suggested as possible shower identification. The KSE shower has been listed as an established shower for years, while PSR#839 was detected during a survey of the CAMS orbits as available until 2016 (Jenniskens et al., 2018).

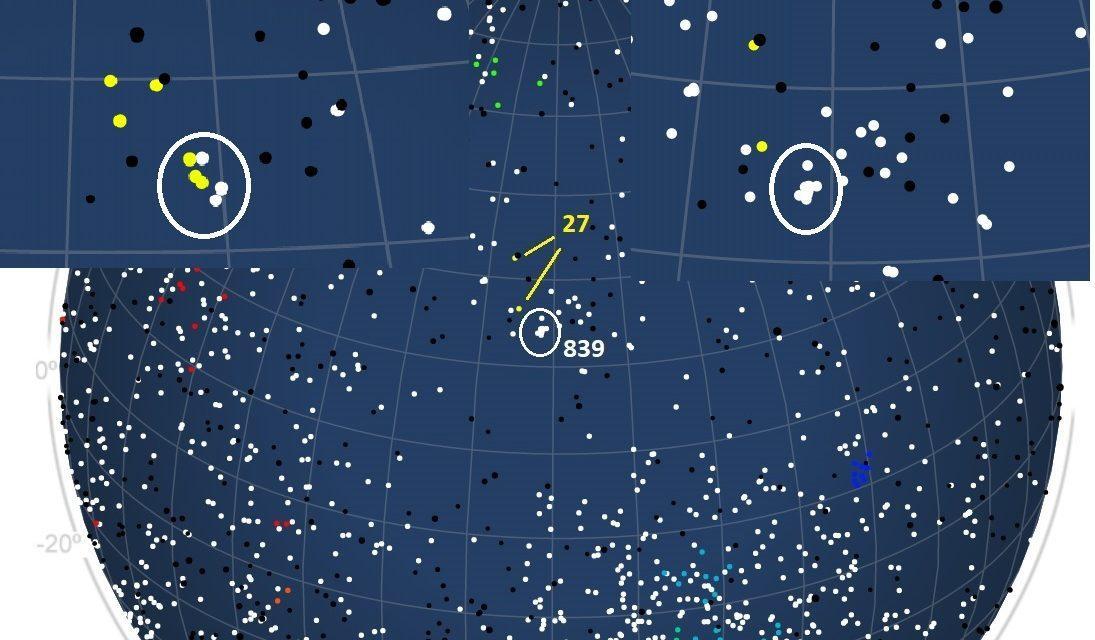
Figure 1 – The radiant map for CAMS for 2020 April 15 with some KSE radiants and the compact PSR radiant nearby. The inset at left shows the compact radiant according to GMN and the inset at right shows the radiant as found by CAMS.
The reference orbits from the IAU working list (https://www.ta3.sk/IAUC22DB/MDC2007/Roje/roje_lista.php?corobic_roje=0&sort_roje=0) of meteor showers are listed in Table 1. The velocity is about identical and the radiant positions are close to each other. Figure 1 shows the situation as registered this year on April 15 by the CAMS networks. The insets compare the compact radiant for the Global Meteor Network with CAMS.
Table 1 – The reference orbits listed for the KSE#027 and PSR#839 as listed in the IAU working list of meteor showers.
| KSE#027 Cook 1973 |
KSE#027 Jacchia 1961 |
KSE#027 Jenniskens et al. 2016 |
PSR#839 Jenniskens et al. 2018 |
|
| λʘ | 15.7° | 15.7° | 20.0° | 25.1° |
| αg | 230.6° | 232.6° | 240.2° | 242.2° |
| δg | +17.8° | +15.4° | +16.8° | +14.0° |
| vg | 45 km/s | 45.0 km/s | 46.7 km/s | 46.3 km/s |
| a | ꝏ | 41.7 AU | 7.9 AU | ꝏ |
| q | 0.45 AU | 0.417 AU | 0.489 AU | 0.435 AU |
| e | 1.00 | – | 0.971 | 1.017 |
| ω | 275° | 279.9° | 273.4° | 277.2° |
| Ω | 15.7° | 16.5° | 20.1° | 25.1° |
| i | 65° | 63.0° | 72.5° | 69.9° |
| N | 4 | 1 | 21 | 5 |
The status of the κ Serpentids (KSE#027) as an established shower raises some questions. Cook (1973) obtained his data from four graphically reduced meteors (McCrosky and Posen, 1961), with limited accuracy. The second reference orbit (Jacchia and Whipple, 1961) is based on a single orbit, a rather questionable criterium to define a reference orbit for a meteor shower. The third reference orbit has been obtained from the CAMS dataset 2010–2013. Looking at the 21 orbits on which the KSE reference orbit is based, some of these orbits fit better with the φ-Serpentids (PSR#839) reference orbit. When the 2016 reference orbit for the κ Serpentids (KSE#027) was calculated the φ-Serpentids (PSR#839) was not yet known. When we calculate the median values for all parameters of these 21 KSE-orbits, we find 242.7° as R.A. instead of the 240.2° listed in the IAU shower list. This orbit is remarkable similar to that of the φ-Serpentids (PSR#839). The only significant difference between both is the time of activity, reflected in the difference in the ascending node Ω.
It looks like we have a dispersed meteor shower with orbits that define the κ Serpentids (KSE#027) followed by a compact component known as the φ-Serpentids (PSR#839). The similarity of both orbits suggests both are somehow related, probably from the same parent body. May be this is an old dispersed shower (KSE#027) with a compact dust trail now observed as the φ-Serpentids (PSR#839) moving perhaps ahead of a parent comet that has still to be discovered? Future observations can learn us whether the enhanced activity in 2020 is just a lucky encounter with a dust concentration in the shower, or the beginning of a trail which will become more active year after year?
2 CAMS BeNeLux
April 14–15 had an almost complete clear night for the CAMS BeNeLux network. All the operational cameras were recording this night. The data of 63 cameras got collected within 24 hours when the next morning Peter Jenniskens reported that the CAMS Namibia network had recorded enhanced activity from a radiant in the top of the constellation Serpens. The next day, data of 73 cameras was available for analyses and yes, CAMS BeNeLux had also registered a few orbits of this meteor shower. The results for CAMS BeNeLux are listed in Table 2. The camera operators who were lucky to contribute to these orbits were: Koen Miskotte (CAMS 354, Ermelo, the Netherlands), Adriana and Paul Roggemans (RMS 3830, Mechelen, Belgium), Hervé Lamy (CAMS 394, Dourbes, Belgium), Luc Gobin (CAMS 390 and 808, Mechelen, Belgium), Guiseppe Canonaco (RMS 3815, Genk, Belgium) and Tioga Gulon (CAMS 3900, Nancy, France).
All CAMS BeNeLux and Namibia PSR orbits were recorded from a very compact radiant area in a short time interval within the range of 25.21° < λʘ < 25.39°, which corresponds to about as little as 4 hours in time. All CAMS networks together had a total of 14 PSR orbits this year. The mean orbit for the 2020 PSR orbits is listed in Table 5 and refers to a thusfar unknown long periodic comet according to Jenniskens (2020). The mean orbit obtained by the CAMS networks agrees very well with that obtained independently by the Global Meteor Network.

Figure 2 – The PSR#839 meteor of April 15, 0h39m27.7s UT, registered by Luc Gobin in Mechelen, Belgium. Note at the top of the picture the CAMS software suggests KSE as possible shower association.
Table 2 – The three PSR orbits obtained by CAMS BeNeLux.
| 14 April 22h53m47.8s |
15 April 0h39m27.7s |
15 April 0h45m18.5s |
|
| λʘ | 25.17° | 25.24° | 25.25° |
| αg | 242.0 ± 0.2° | 242.3 ± 0.0° | 241.9 ± 0.2° |
| δg | +12.7 ± 0.3° | +14.1 ± 0.1° | +14.1 ± 0.2° |
| vg | 42.8 ± 0.3 km/s | 44.8 ± 0.1 km/s | 46.6 ± 0.1 km/s |
| Hb | 101.2 km | 107.2 km | 105.5 km |
| He | 92.9 km | 85.8 km | 90.8 km |
| a | 4.26 AU | 14.7 AU | ꝏ |
| q | 0.3908 AU | 0.4308 AU | 0.489 AU |
| e | 0.9082 | 0.9707 | 1.0368 |
| ω | 286.41° | 279.12° | 276.01° |
| Ω | 25.17° | 25.24° | 25.25° |
| i | 65.1° | 67.9° | 69.6° |
| Camera | 354–3830 | 394–390 | 808–3900–3815 |
3 Global Meteor Network
We checked the results of the Global Meteor Network for the night 14–15 April (https://globalmeteornetwork.org/data/traj_summary_data/daily/traj_summary_20200414_solrange_025.0-026.0.txt). All the raw trajectory and orbit data are made available online after 24 hours. The GMN radiants can also be compared online (http://cams.seti.org/FDL/index-GMN.html). We found 9 candidates, six were identified by the analyzing software as PSR, three were classified as KSE. Some of the PSR orbits recorded by the Global Meteor Network appeared several hours later than those recorded by CAMS BeNeLux and CAMS Namibia. The orbit identification was checked with the similarity criterion DD of Drummond (1981) using the orbits given by Jenniskens (2016, 2018) as reference, listed in Table 1. The meteors and cameras involved are listed in Table 3.
Figure 3 – The φ-Serpentids (PSR#839) meteor recorded on 15 April at 0h45m18.5s by camera 003815 in Genk, Belgium (Adriana and Paul Roggemans).
The meteor of 01h35m02.2s fails to fit the PSR reference orbit, the meteors of 05h50m48.0s and 05h50m48.0s have a best fit with the KSE reference orbit but also fit the PSR orbit. The meteor of 05h43m49.5s is listed as best fit with PSR but also fits the KSE orbit.
The cameras marked with BE share a part of the same layers of the atmosphere with the cameras of the CAMS BeNeLux network. The PSR meteor on BE0003 at 23h29m23s was not found at any other CAMS station, but on two French RMS cameras of GMN. The PSR meteor on BE0003 at 0h45m18s (Figure 3) had no partner camera within the GMN. The PSR meteor on BE0001 and BE0002 at 03h17m54s (Figures 4 and 5) for some reason did not pass the Coincidence procedure of CAMS. This proves how valuable complementary CAMS and GMN really work.
Table 3 – The Global Meteor Network candidate orbits for PSR shower association. The records marked in yellow have better similarity with the KSE reference orbit.
| Beginning | IAU | DD | Participating |
| 2020-04-14 23h29m23.1s | 839 | 0.01 | BE3-FR6-FRG |
| 2020-04-15 01h24m00.9s | 839 | 0.05 | HRD-HR10-IT1 |
| 2020-04-15 01h35m02.2s | 27 | 0.07 | FR6-FRG |
| 2020-04-15 03h17m54.3s | 839 | 0.02 | BE1-BE2 |
| 2020-04-15 05h43m49.5s | 839 | 0.09 | US6-US8 |
| 2020-04-15 05h50m48.0s | 27 | 0.06 | US7-US8-USA |
| 2020-04-15 06h24m20.6s | 839 | 0.08 | US7-US8-USA-USC-USE-USH |
| 2020-04-15 07h52m53.2s | 839 | 0.06 | CA6-CA9-CA15 |
| 2020-04-15 09h25m26.5s | 27 | 0.02 | US4-US5-USC-USD-USH |
When we calculate the mean orbit based on the 6 certain PSR meteors using the method of Jopek et al. (2006), we find a mean orbit which is in good agreement with the result obtained by Peter Jenniskens based on the CAMS data, see Table 5.

Figure 4 – The φ-Serpentids (PSR#839) meteor recorded on 15 April at 3h17m54.3s by camera BE0002 in Mechelen, Belgium (Adriana and Paul Roggemans).
Figure 5 – The φ-Serpentids (PSR#839) meteor recorded on 15 April at 3h17m54.3s by camera BE0001 in Grapfontaine, Belgium (Adriana and Paul Roggemans).
4 SonotaCo Network Japan
The SonotaCo camera network found 6 candidate orbits:
- A: 2020 April 11 18h30m27s UT maga = +1.0
- B: 2020 April 14 12h05m12s UT maga = –2.7
- C: 2020 April 14 12h14m55s UT maga = –0.1
- D: 2020 April 14 18h55m58s UT maga = +0.9
- E: 2020 April 15 15h05m31s UT maga = –1.7
- F: 2020 April 15 16h29m01s UT maga = +0.4
Table 4 – The orbits obtained by the SonotaCo Network.
| A | B | C | D | E | F | |
| λʘ | 22.1° | 24.7° | 24.7° | 25.0° | 25.8° | 25.9° |
| αg | 234.0° | 241.8° | 239.6° | 242.3° | 240.2° | 236.9° |
| δg | +11.6° | +13.9° | +15.9° | 13.4° | 17.9° | 12.7° |
| vg | 39.8 | 45.6 | 39.5 | 42.8 | 39.6 | 38.3 |
| Hb | 89.4 | 99.8 | 93.6 | 101.8 | 98.2 | 92.1 |
| He | 85.9 | 88.0 | 82.7 | 97.8 | 86.5 | 87.6 |
| a | 3.7 | 54.4 | 3.3 | 4.3 | 4.3 | 3.2 |
| q | 0.36 | 0.43 | 0.45 | 0.41 | 0.49 | 0.40 |
| e | 0.90 | 0.99 | 0.87 | 0.91 | 0.89 | 0.88 |
| ω | 290.6° | 278.7° | 281.4° | 284.6° | 275.0° | 287.2° |
| Ω | 22.1° | 24.7° | 24.7° | 25.0° | 25.8° | 25.9° |
| i | 54.1° | 68.9° | 58.0° | 65.5° | 57.8° | 51.9° |
Table 5 – Comparing the PSR orbits obtained by CAMS, by GMN and by SonotaCo Network.
| CAMS | GMN | SonotaCo | |
| λʘ | 25.2° | 25.4° | 25.2° |
| αg | 242.4 ± 0.4° | 242.3 ± 0.7° | 240.2° |
| δg | +13.9 ± 0.3° | +14.1 ± 0.8° | +14.8° |
| vg | 46.4 ± 0.5 km/s | 44.5 ± 2.3 km/s | 41.1 km/s |
| Hb | – | 104.3 ± 2.1 km | 97.1 km |
| He | – | 90.7 ± 2.6 km | 88.5 km |
| a | ꝏ | 72 AU | 13.9 AU |
| q | 0.432 ± 0.007 AU | 0.432 ± 0.02 AU | 0.4 AU |
| e | 1.011 ± 0.034 | 0.994 ± 0.08 | 0.9 |
| ω | 277.6 ± 1.2° | 277.92 ± 4.9° | 281.4° |
| Ω | 25.24 ± 0.13° | 25.395° | 25.2° |
| i | 69.7 ± 0.7° | 68.3 ± 3.1° | 60.4° |
| N | 12 | 6 | 5 |
The orbit of meteor B is very similar to the mean orbit obtained for the PSR#839 orbits by CAMS and GMN. The other orbits are more spread and all have a lower geocentric velocity vg. As mentioned above the first alert came from orbits recorded in about 4 hours time. All PSR orbits from the compact radiant were collected in less than 24 hours of time. The meteor at April 14 12h05m12s UT detected by the SonotaCo Network may be one of the earliest meteors of the compact PSR return. Some of the meteors detected by the SonotaCo Network may belong to the more dispersed component. This could explain the lower velocity vg, smaller eccentricity e and lower inclination i of the mean orbit.
5 The KSE#027 and PSR#839 confusion
Both KSE#027 and especially PSR#839 are poorly documented. No activity period is determined and while we got a reliable reference orbit for PSR#839 from a compact cluster of orbits, the reliability of the reference orbits for the obviously very dispersed κ Serpentid shower remains questionable. Two showers with nearby radiants, the same velocity and only 5° apart in solar longitude, how to identify these orbits correctly? Are both somehow related?
This confusing situation has been discussed before in a study by Masahiro Koseki (2019). Masahiro Koseki considers the positions of shower radiants in Sun centered ecliptic coordinates relative to the median value of the radiant position. By counting the number of radiants that occur within concentric circles and radiant density ratios in function of the time (solar longitude) the evidence for the existence of the shower can be evaluated. The study by Masahiro Koseki includes two other nearby minor showers, the April β Herculids (ABH#836) and the δ Herculids (DHE#841) with nearby radiants but significant higher geocentric velocities. The conclusion is that no clear concentration could be found for the κ Serpentid shower and the question then is how KSE got ranked as an established shower? The φ-Serpentids (PSR#839) displays a small but clear peak and its radiant position is close to that of KSE.
The available orbits may help to get a better picture of the situation. We have 1101924 orbits public available, 630341 combined for EDMOND and SonotaCo (2007–2019), 471583 for CAMS (2010–2016). We use the orbit given for KSE#027 by Jenniskens et al. (2016) as reference (Table 1) and for PSR#839 the orbit of Global Meteor Network as reference (see Table 5). These reference orbits are used to search for orbits that fulfil the D-criteria of Southworth and Hawkins (1963), Drummond (1981) and Jopek (1993) combined. We define five different classes with specific threshold levels of similarity:
- Low: DSH < 0.25 & DD < 0.105 & DH < 0.25;
- Medium low: DSH < 0.2 & DD < 0.08 & DH < 0.2;
- Medium high: DSH < 0.15 & DD < 0.06 & DH < 0.15;
- High: DSH < 0.1 & DD < 0.04 & DH < 0.1.
- Very high: DSH < 0.05 & DD < 0.02 & DH < 0.05.
Working with the discrimination criteria requires caution. The results indicate only a degree of similarity between the orbits. D-criteria provide no prove for any physical relationship between the meteoroids. D-criteria can be very misleading, especially if applied on short period orbits with small eccentricity. In case of the KSE and PSR which have long period orbits with high eccentricity and high inclination the use of D-criteria is justified. However, the method should be applied unbiased and we must be confident that the orbits are based on reliable velocities. Although the 2020 PSR activity suggests a very narrow concentrated shower, we cannot apriory exclude that more dispersed orbits are related to this shower. It should be understood that the low threshold class of similarity may be contaminated by sporadics that fulfil the criteria by pure chance. The purpose is to check if a shower concentration is confirmed by the high threshold classes with very similar orbits.
Table 6 – Number of low and high threshold KSE and PSR orbits per year.
| Year | KSE Low |
KSE High |
PSR Low |
PSR High |
| 2007 | 5 | 1 | 5 | 1 |
| 2008 | 6 | 1 | 4 | 0 |
| 2009 | 12 | 0 | 3 | 1 |
| 2010 | 2 | 0 | 3 | 1 |
| 2011 | 28 | 2 | 17 | 1 |
| 2012 | 22 | 0 | 17 | 4 |
| 2013 | 47 | 0 | 31 | 7 |
| 2014 | 51 | 6 | 34 | 6 |
| 2015 | 52 | 2 | 36 | 5 |
| 2016 | 42 | 2 | 29 | 2 |
| 2017 | 11 | 0 | 7 | 1 |
| 2018 | 5 | 0 | 4 | 0 |
| 2019 | 10 | 0 | 6 | 2 |
| Total | 293 | 14 | 196 | 31 |
We find 293 KSE and 196 PSR orbits that fulfil at least the low similarity class mentioned above. This may be misleading somehow because of the risk for false positives. Therefore, we also list the number of orbits that fulfil the high threshold criteria in Table 6. Considering the high threshold class, the PSR shower emerges much stronger than the KSE which remains absent in most years. The number of high threshold PSR orbits registered in 2020 exceeds all previous years.
The number of orbits per year depends mainly on the number of available data. Before 2011 only EDMOND and SonotaCo Network orbits are available, after 2016 only SonotaCo Network orbits. There is no indication for any periodicity. Looking at the number of orbits in each class of similarity threshold we see that the KSE orbits appear very scattered while the PSR shower shows a distinct concentration of orbits (Table 7).
Table 7 – Number of KSE and PSR orbits per similarity class.
| Class | KSE | PSR |
| Low | 293 | 196 |
| Medium low | 147 | 99 |
| Medium high | 73 | 53 |
| High | 14 | 31 |
| Very high | 0 | 17 |
The KSE orbits were detected in the time range 6.3° < λʘ < 33.5° for the low threshold, 16.8° < λʘ < 24.9° for the high threshold with not a single orbit fulfilling the very high threshold. For the PSR the time range was 12.8° < λʘ < 37.4° for the low threshold, 23.5° < λʘ < 27.0° for the very high threshold. These periods are a good indication for the activity periods of these showers. In a future case study, we may attempt to run an iterative search to locate orbit concentrations to determine independently new reference orbits.
We consider the radiant distribution in Sun centered ecliptic coordinates to mark each radiant either as KSE or as PSR with a different color according to the threshold class of similarity. In Figure 6 we see how complex the picture really is. KSE radiants appear mainly north and east from the PSR radiants, but a large number of the orbits fit the discrimination criteria for both shower reference orbits. This becomes better visible if we display only the radiants of orbits that fit the D-criteria for the KSE reference in Figure 7 and only those that match the PSR reference in Figure 8. We see the PSR orbits (circles in Figure 8) fit the criteria for the KSE reference (triangles in Figure 7) and not only for the low threshold class. We make the same presentation in another distribution with the inclination i against the length of perihelion Π in Figures 9, 10 and 11.

Figure 6 – Radiant positions for all KSE and PSR orbits in Sun centered ecliptic coordinates, color coded for the different similarity classes of the combined D-criteria.

Figure 7 – Radiant positions for the KSE orbits in Sun centered ecliptic coordinates, color coded for the different similarity classes of the combined D-criteria.

Figure 8 – Radiant positions for the PSR orbits in Sun centered ecliptic coordinates, color coded for the different similarity classes of the combined D-criteria.

Figure 9 – Plot of inclination i against length of perihelion Π for all KSE and PSR orbits, color coded for the different similarity classes of the combined D-criteria.

Figure 10 – Plot of inclination against length of perihelion Π for the KSE orbits, color coded for the different similarity classes of the combined D-criteria.

Figure 11 – Plot of inclination against length of perihelion Π for the PSR orbits, color coded for the different similarity classes of the combined D-criteria.
The KSE radiants appear very dispersed and only the PSR radiants show a very distinct concentration. There seems to be no objective way to distinguish KSE and PSR associations. In Figures 6, 7 and 8 we see a dispersed concentration (at left) and a more concentrated one a bit lower right of it. This looks like two showers, but when we take the D-criteria into account, it becomes obvious there is a lot of overlap with orbits that fit both shower associations. In Figures 9, 10 and 11 the radiants also appear very dispersed, the best KSE associations appear to have a slightly higher inclination and lower value for the length of perihelion Π than the best PSR orbits.

Figure 12 – Plot of the ecliptic latitude β (°) against the Sun centered longitude λ – λʘ (°) for the 147 KSE orbits that fulfill the medium low threshold similarity criteria with a color gradient to display the variation in the velocity vg.

Figure 13 – Plot of the ecliptic latitude β (°) against the Sun centered longitude λ – λʘ (°) for the 99 PSR orbits that fulfill the medium low threshold similarity criteria with a color gradient to display the variation in the velocity vg.

Figure 14 – Plot of inclination i (°) against the length of perihelion П (°) for the 147 KSE orbits that fulfill the medium low threshold similarity criteria with a color gradient to display the variation in the velocity vg.

Figure 15 – Plot of inclination i (°) against the length of perihelion П (°) for the 99 PSR orbits that fulfill the medium low threshold similarity criteria with a color gradient to display the variation in the velocity vg.
In Figures 12 and 13 we look at the velocity distribution in the Sun centered ecliptic coordinates. To reduce the number of false positives that may still be included in the low threshold class, we used the medium low class orbits. Here we see for both KSE and PSR associated radiants slower velocities for radiants in the western part (at left) and higher velocities in the eastern part (at right) towards the Apex. Note that both the dispersed KSE radiants and the concentrated PSR radiants appear in the same velocity range in both plots.
The same picture emerges in the plots of inclination i (°) against the length of perihelion П (°) (Figures 14 and 15). Here the dispersed KSE orbits appear at slightly higher inclination with a higher velocity while the PSR concentration is situated at a bit lower inclination but within the same velocity range as the KSE orbits.
The question arises if the reference orbit for KSE we took from Jenniskens et al. (2016) is a good reference, this orbit may have been derived from a mixture of KSE and PSR orbits, as the PSR shower was not yet known when the 2016 mean orbits were calculated. The similarity between both KSE and PSR orbits makes it difficult, if not impossible to distinguish both with any degree of certainty.
6 Conclusion
A sudden short-lived activity enhancement of the φ-Serpentids (PSR#839) shower resulted in a number of orbits from a very narrow radiant concentration registered within a short time interval. The identification from simple radiant positions and velocities of the meteors caused confusion with the nearby κ Serpentids (KSE#027), an established but nevertheless poorly documented meteor stream. Looking up PSR and KSE orbits in our database with 1101924 public available orbits, both showers display considerable overlapping. This confirms an earlier detailed study by Masahiro Koseki (2019). While the φ-Serpentids (PSR#839) appear to be a very distinct concentration of similar orbits, the question arises if the available KSE reference orbits are relevant as these may be partially based on PSR orbits and perhaps some other nearby sources as the shower was not known when the KSE reference orbits were derived.
If we consider the φ-Serpentids (PSR#839) as a distinct minor shower, the KSE orbits may be related to it as a very dispersed component of this shower. The recent enhanced activity from the compact radiant of the φ-Serpentids is likely related to an unknown long periodic comet and could be caused by dust moving ahead of its parent body, announcing its return. Both the φ-Serpentids (PSR#839) and κ Serpentids (KSE#027) are very likely related and may have a common origin. It is highly recommended to keep an eye on the the φ-Serpentids activity in the future and it is very disrable to make a dedicated case study to check if a better representative reference orbit can be found for the KSE component.
Acknowledgment
The authors wish to thank Peter Jenniskens for providing the information of CBET 4756. We thank Masahiro Koseki for his very valuable feedback and we thank Denis Vida for providing the scripts to plot the velocity distribution with a color gradient and to compute the average orbit according to the method of Jopek et al. (2006).
We used the data of the Global Meteor Network (https://globalmeteornetwork.org/data/) which is released under the CC BY 4.0 license (https://creativecommons.org/licenses/by/4.0/). We thank the SonotaCo Network members in Japan who have been observing every night for more than 10 years, making it possible to consult their orbits. We thank the camera operators of the CAMS (http://cams.seti.org/) networks (http://cams.seti.org/FDL/). And we thank the contributors to EDMOND (https://fmph.uniba.sk/microsites/daa/daa/veda-a-vyskum/meteory/edmond/), including: BOAM (Base des Observateurs Amateurs de Meteores, France), CEMeNt (Central European Meteor Network, cross-border network of Czech and Slovak amateur observers), CMN (Croatian Meteor Network or HrvatskaMeteorskaMreza, Croatia), FMA (Fachgruppe Meteorastronomie, Switzerland), HMN (HungarianMeteor Network or Magyar Hullocsillagok Egyesulet, Hungary), IMO VMN (IMO Video Meteor Network), MeteorsUA (Ukraine), IMTN (Italian amateur observers in Italian Meteor and TLE Network, Italy), NEMETODE (Network for Meteor Triangulation and Orbit Determination, United Kingdom), PFN (Polish Fireball Network or Pracownia Komet i Meteorow, PkiM, Poland), Stjerneskud (Danish all-sky fireball cameras network, Denmark), SVMN (Slovak Video Meteor Network, Slovakia), UKMON (UK Meteor Observation Network, United Kingdom).
The authors thank Peter Jenniskens, Masahiro Koseki and Denis Vida for the verification of this article and for their valuable comments and suggestions.
References
Cook A. F. (1973). “A Working List of Meteor Streams”. In, Curtis L. Hemenway, Peter M. Millman, and Allan F. Cook, editors, Evolutionary and Physical Properties of Meteoroids, Proceedings of IAU Colloq. 13, held in Albany, NY, 14-17 June 1971. National Aeronautics and Space Administration SP 319, 1973, pages 183–191.
Drummond J. D. (1981). “A test of comet and meteor shower associations”. Icarus, 45, 545–553.
Jacchia, Luigi G., Whipple, Fred L. (1961). “Precision Orbits of 413 Photographic Meteors”. Smithsonian Contributions to Astrophysics, 4, 97–129.
Jenniskens P., Nénon Q., Albers J., Gural P. S., Haberman B., Holman D., Morales R., Grigsby B. J., Samuels D. and Johannink C. (2016). “The established meteor showers as observed by CAMS”. Icarus, 266, 331–354.
Jenniskens P., Baggaley J., Crumpton I., Aldous P., Pokorny P., Janches D., Gural P. S., Samuels D., Albers J., Howell A., Johannink C., Breukers M., Odeh M., Moskovitz N., Collison J. and Ganjuag S. (2018). “A survey of southern hemisphere meteor showers”. Planetary Space Science, 154, 21–29.
Jenniskens P. (2020). “Phi Serpentid meteor shower”. CBET 4756.
Jopek T. J. (1993). “Remarks on the meteor orbital similarity D-criterion”. Icarus, 106, 603–607.
Jopek T. J., Rudawska R. and Pretka-Ziomek H. (2006). “Calculation of the mean orbit of a meteoroid stream”. Monthly Notices of the Royal Astronomical Society, 371, 1367–1372.
Koseki Masahiro (2019). “Legendary meteor showers: studies on Harvard photographic results”. WGN, Journal of the International Meteor Organization, 47, 139–150.
McCrosky R. E. and Posen A. (1961). “Orbital elements of photographic meteors”. Smithson. Contrib. Astrophys., 4, 15–84.
Southworth R. R. and Hawkins G. S. (1963). “Statistics of meteor streams”. Smithson. Contrib. Astrophys., 7, 261–286.